Úplný metrický prostor

V matematice, úplný metrický prostor je metrický prostor, ve kterém každý Cauchyova posloupnost je konvergentní. Jinými slovy, každá Cauchyova posloupnost v metrickém prostoru má tendenci v limitu k bodu, který je opět prvkem tohoto prostoru. Metrický prostor je tedy v jistém smyslu ” kompletní.”

• 1 Formální definice
• 2 Příklady
• 3 Dokončení
  • 3.1 Příklady
• 4 Topologicky úplný prostor
• 5 Viz také

Formální definice

Nechť X je metrický prostor s metrikou d. Pak X je úplný, pokud pro každou Cauchyova posloupnost 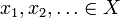je element 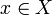takové, že .

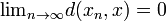příklady

• reálná čísla R a obecněji konečné rozměrné euklidovské prostory s obvyklou metrikou jsou kompletní.
• jakýkoli kompaktní metrický prostor je postupně kompaktní a tudíž úplný. Converse nedrží: například R je kompletní, ale není kompaktní.
• V prostoru s diskrétní metrikou, jen Cauchyho posloupnosti jsou ty, které jsou konstantní z nějakého bodu. Proto je jakýkoli diskrétní metrický prostor kompletní. Některé ohraničené úplné metrické prostory tedy nejsou kompaktní.
• racionální čísla Q nejsou úplná. Například posloupnost (xn) definována x0 = 1, xn+1 = 1 + 1/xn je Cauchyova, ale nekonverguje v Q (V R konverguje k iracionální číslo.)

Dokončení

Každý metrický prostor X má dokončení 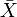což je úplný metrický prostor, ve kterém X je izometricky vložené jako hustý podprostor. Dokončení má univerzální vlastnost.

Příklady

• reálná čísla R jsou dokončení racionální čísla Q, s ohledem na obvyklé metriky absolutní vzdálenost.

Topologicky úplný prostor

Úplnost není topologická vlastnost: je možné, úplný metrický prostor, aby homeomorphic k metrický prostor, který není úplný. Například reálná přímka R je homeomorfní na otevřený interval, řekněme (0,1). Jiný příklad: map

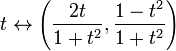
je homeomorfizmus mezi úplný metrický prostor R a neúplné prostoru, což je jednotková kružnice v Euklidovské rovině s bodem (0,-1) zrušuje. Ten prostor není kompletní jako non-Cauchyova posloupnost odpovídající t=n, n vede přes pozitivní celá čísla je mapována na non-Cauchyova posloupnost konvergentní na kruhu.

můžeme definovat topologické prostor, být metricky topologicky úplný, pokud je homeomorphic k úplný metrický prostor. Topologické podmínkou pro tuto vlastnost je, že prostor bude metrizovatelné a absolutní Gδ, že je Gδ v každé topologické prostor, ve kterém může být vložen (nebo jen Gδ v jeho dokončení ve zvolené metriky). Zejména všechny otevřené podmnožiny euklidovských prostorů jsou metricky topologicky kompletní.

Viz také

• Banachova prostoru
• Hilbertův prostor

Některé materiály na této stránce mohou dříve objevily na Citizendium.