4.1: kinetisk energi
kinetisk energi i kollisioner
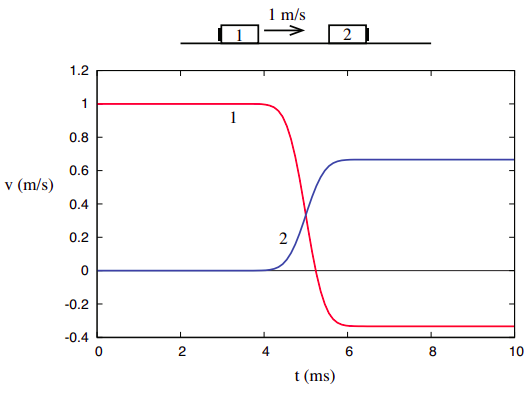
for at få nogle yderligere indsigt i begrebet kinetisk energi, og de måder, hvorpå det er forskelligt fra momentum, er det nyttigt at se på det i samme indstilling, hvor vi “opdagede” momentum, nemlig endimensionelle kollisioner i et isoleret system. Hvis vi igen ser på kollisionen repræsenteret i figur 3.1.1 i kapitel 3, gengivet nedenfor,
\
Bemærk at 1/18 + 4/9 = 9/18 = 1/2, og så
\
med ord finder vi, at i denne kollision er den endelige værdi af den samlede kinetiske energi den samme som dens oprindelige værdi, og det ser ud til, at vi har “opdaget” en anden konserveret mængde (udover momentum) for dette system.
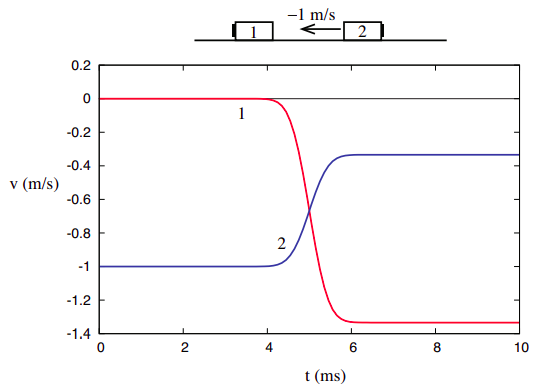
denne tro kan styrkes, hvis vi ser næste på kollisionen afbildet i figur 3.1.2 i kapitel 3, igen gengivet nedenfor. Husk jeg påpegede dengang, at vi kan tænke på dette som virkelig den samme kollision som afbildet i figur 3.1.1, kun kigget på fra en anden referenceramme (en bevæger sig oprindeligt til højre ved 1 m/s). Vi vil have mere at sige om, hvordan man omdanner mængder fra en referenceramme til en anden i slutningen af kapitlet.
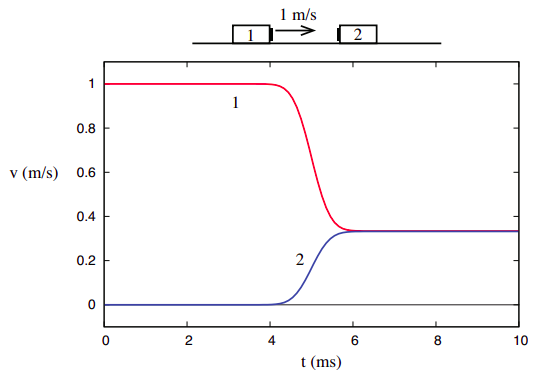
tingene er dog meget forskellige, når vi overvejer det tredje kollisionseksempel vist i kapitel 3, nemlig det, hvor de to objekter sidder fast sammen efter kollisionen.
\
hvad dette viser, er imidlertid, at i modsætning til det samlede momentum i et system, som er fuldstændig upåvirket af interne interaktioner, afhænger den samlede kinetiske energi af detaljerne i interaktionen og formidler således nogle oplysninger om dens natur. Vi kan derefter forfine vores undersøgelse af kollisioner for at skelne mellem to slags: dem, hvor den oprindelige kinetiske energi genvindes efter kollisionen, som vi vil kalde elastisk, og dem, hvor den ikke er, som vi kalder uelastisk. Et specielt tilfælde af uelastisk kollision er den, der kaldes helt uelastisk, hvor de to objekter ender sammen, som i figur \(\Sideindeks{3}\). Som vi skal se senere, er det kinetiske energi “underskud” størst i så fald.
jeg har sagt ovenfor, at den kinetiske energi i en elastisk kollision “genvindes”, og jeg foretrækker denne terminologi frem for “konserveret”, fordi den samlede kinetiske energi i et system faktisk ikke forbliver konstant i hele interaktionen, ikke engang under en elastisk kollision. Det enkleste eksempel for at vise dette ville være en elastisk, head-on kollision mellem to objekter af samme masse, der bevæger sig med samme hastighed mod hinanden. I løbet af kollisionen bringes begge objekter øjeblikkeligt til ophør, før de vender retning og hopper tilbage, og i det øjeblik er den samlede kinetiske energi nul.
du kan også undersøge tallene \(\Sideindeks{1}\) og \(\Sideindeks{2}\) ovenfor og beregne fra graferne værdien af den samlede kinetiske energi under kollisionen. Du vil se, at det falder til et minimum og derefter vender tilbage til dets oprindelige værdi (Se også Figur \(\Sideindeks{4}\), senere i dette kapitel). Konventionelt kan vi tale om kinetisk energi som “bevaret” i elastiske kollisioner, men det er vigtigt at indse, at vi ser på en anden slags “bevarelse” end hvad vi havde med det samlede momentum, som var konstant før, under og efter interaktionen, så længe systemet forblev isoleret.
elastiske kollisioner antyder, at uanset den ultimative karakter af denne ting, vi kalder “energi”, kan det være muligt at opbevare den i en eller anden form (i dette tilfælde i løbet af kollisionen) og derefter genvinde den som kinetisk energi til sidst. Dette baner vejen for indførelsen af andre former for “energi” udover kinetisk energi, som vi skal se i et senere kapitel, og muligheden for interkonversion at finde sted blandt disse slags. For øjeblikket skal vi blot sige, at i en elastisk kollision lagres en vis mængde kinetisk energi midlertidigt som en slags “intern energi”, og efter kollisionen omdannes dette tilbage til kinetisk energi; hvorimod i en uelastisk kollision omdannes en vis mængde kinetisk energi uigenkaldeligt til en eller anden “intern energi”, og vi får den aldrig tilbage.
da det, der i sidste ende sker, afhænger af detaljerne og arten af interaktionen, vil vi blive ført til at skelne mellem “konservative” interaktioner, hvor kinetisk energi reversibelt opbevares som en anden form for energi et eller andet sted, og “dissipative” interaktioner, hvor energikonverteringen i det mindste delvist er irreversibel. Det er klart, elastiske kollisioner er forbundet med konservative interaktioner, og uelastiske kollisioner er forbundet med dissipative interaktioner. Denne foreløbige klassificering af interaktioner skal dog gennemgås lidt mere omhyggeligt i næste kapitel.