komplet metrisk rum

i matematik er et komplet metrisk rum et metrisk rum, hvor hver Cauchy-sekvens er konvergent. Med andre ord har hver Cauchy-sekvens i det metriske rum tendens til grænsen til et punkt, der igen er et element i dette rum. Derfor er det metriske rum på en måde ” komplet.”

• 1 formel definition
• 2 Eksempler
• 3 færdiggørelse
  • 3.1 eksempler
• 4 topologisk komplet rum
• 5 Se også

formel definition

lad være et metrisk rum med metrisk d. så er det komplet, hvis der for hver Cauchy-sekvens 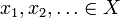er et element 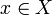sådan at .

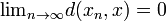eksempler

• de reelle tal R og mere generelt endelige dimensionelle euklidiske rum med den sædvanlige metriske er komplette.
• ethvert kompakt metrisk rum er sekventielt kompakt og dermed komplet. Det omvendte holder ikke: for eksempel er R komplet, men ikke kompakt.
• i et rum med den diskrete metric er de eneste Cauchy-sekvenser dem, der er konstante fra et tidspunkt. Derfor er ethvert diskret metrisk rum komplet. Således er nogle afgrænsede komplette metriske rum ikke kompakte.
• de rationelle tal er ikke komplette. For eksempel er sekvensen defineret af H0 = 1, hn+1 = 1 + 1/HN Cauchy, men konvergerer ikke i K. (I R konvergerer den til et irrationelt tal.)

afslutning

hvert metrisk rum har en færdiggørelse 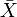, som er et komplet metrisk rum, hvor det er isometrisk indlejret som et tæt underrum. Færdiggørelsen har en universel ejendom.

eksempler

• de reelle tal R er færdiggørelsen af de rationelle tal k i forhold til den sædvanlige metriske absolutte afstand.

topologisk komplet rum

fuldstændighed er ikke en topologisk egenskab: det er muligt for et komplet metrisk rum at være homomorf til et metrisk rum, som ikke er komplet. For eksempel er den virkelige Linje R homeomorf til et åbent interval, siger (0,1). Et andet eksempel: kortet

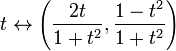
er en homeomorfisme mellem Det komplette metriske rum R og det ufuldstændige rum,som er enhedscirklen i det euklidiske plan med punktet (0, -1) slettet. Sidstnævnte rum er ikke komplet, da den ikke-Cauchy-sekvens svarende til t=n, Når n løber gennem de positive heltal, kortlægges til en ikke-konvergent Cauchy-sekvens på cirklen.

vi kan definere et topologisk rum, der skal metrisk topologisk udfyldes, hvis det er homomorf til et komplet metrisk rum. En topologisk betingelse for denne egenskab er, at rummet er metriserbart og en absolut g-kran, det vil sige en G-kran i hvert topologisk rum, hvor det kan indlejres (eller bare G-kran i dets færdiggørelse i en valgt metrisk). Især er alle åbne undergrupper af euklidiske rum metrisk topologisk komplette.

Se også

• Banach space
• Hilbert space

noget indhold på denne side kan tidligere have været vist på borgerskab.