tidssynkronisering i distribuerede systemer

hvis du finder dig bekendt med hjemmesider som facebook.com eller google.med, måske ikke mindre end en gang har du spekuleret på, hvordan disse hjemmesider kan håndtere millioner eller endda titusinder af anmodninger pr. Vil der være en enkelt kommerciel server, der kan modstå denne enorme mængde anmodninger, på den måde, at hver anmodning kan serveres rettidigt for slutbrugere?

når vi dykker dybere ned i denne sag, kommer vi til begrebet distribuerede systemer, en samling af uafhængige computere (eller noder), der ser ud til brugerne som et enkelt sammenhængende system. Denne opfattelse af sammenhæng for brugerne er klar, da de mener, at de har at gøre med en enkelt humongous maskine, der tager form af flere processer, der kører parallelt for at håndtere batches af anmodninger på en gang. Men for folk, der forstår systeminfrastruktur, bliver tingene ikke så lette som sådan.

for tusinder af uafhængige maskiner, der kører samtidigt, der kan spænde over flere tidsområder og kontinenter, skal der gives nogle typer synkronisering eller koordinering for at disse maskiner kan samarbejde effektivt med hinanden (så de kan vises som en). I denne blog vil vi diskutere synkronisering af tid og hvordan det opnår konsistens blandt maskiner på bestilling og årsagssammenhæng af begivenheder.

indholdet af denne blog vil blive organiseret som følger:

1. Ursynkronisering
2. logiske ure
3. Tag væk
4. Hvad er det næste?

fysiske ure

i et centraliseret system er tiden entydig. Næsten alle computere har et “realtidsur” for at holde styr på tiden, normalt synkroniseret med en præcist bearbejdet kvartskrystal. Baseret på den veldefinerede frekvensoscillation af dette kvarts kan en computers operativsystem nøjagtigt overvåge den interne tid. Selv når computeren er slukket eller går ud af opladning, fortsætter kvartset med at krydse på grund af CMOS-batteriet, et lille kraftcenter integreret i bundkortet. Når computeren opretter forbindelse til netværket (Internet), kontakter operativsystemet derefter en timerserver, der er udstyret med en UTC-modtager eller et nøjagtigt ur, for nøjagtigt at nulstille den lokale timer ved hjælp af Netværkstidsprotokol, også kaldet NTP.

selvom denne frekvens af krystalkvarts er rimelig stabil, er det umuligt at garantere, at alle krystaller fra forskellige computere fungerer med nøjagtig samme frekvens. Forestil dig et system med n-computere, hvis hver krystal kører med lidt forskellige hastigheder, hvilket får urene gradvist til at komme ud af synkronisering og give forskellige værdier, når de udlæses. Forskellen i tidsværdierne forårsaget af dette kaldes urskævhed.

under denne omstændighed blev tingene rodet for at have flere rumligt adskilte maskiner. Hvis brugen af flere interne fysiske ure er ønskelig, hvordan synkroniserer vi dem med virkelige ure? Hvordan synkroniserer vi dem med hinanden?

Netværkstidsprotokol

en fælles tilgang til parvis synkronisering mellem computere er ved brug af klientservermodellen, dvs.lad klienter kontakte en tidsserver. Lad os overveje følgende eksempel med 2 Maskiner A og B:

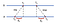
for det første sender A en anmodning tidsstemplet med værdi Ttel til B. B, Når meddelelsen ankommer, registrerer tidspunktet for modtagelse af TFL fra sit eget lokale ur og svar med en besked tidsstemplet med T₂, piggybacking den tidligere registrerede værdi TfL. Endelig, A, efter at have modtaget svaret fra B, registrerer ankomsttidspunktet tort. For at redegøre for tidsforsinkelsen ved levering af meddelelser beregner vi Larsfl = Tflr, Lars₂ = Tflr-T₂. Nu, en estimeret forskydning af en relativ til B er:

baseret på Kurt kan vi enten bremse uret på A eller fastgøre det, så de to maskiner kan synkroniseres med hinanden.

da NTP er parvis anvendelig, kan B ‘ s ur også justeres til A. Det er dog uklogt at justere uret i B, hvis det vides at være mere nøjagtigt. For at løse dette problem opdeler NTP servere i lag, dvs.rangering af servere, så urene fra mindre nøjagtige servere med mindre rækker synkroniseres med de mere nøjagtige servere med højere rækker.

Berkeley algoritme

i modsætning til klienter, der regelmæssigt kontakter en tidsserver for nøjagtig tidssynkronisering, foreslog Gusella og Berkeley i 1989 Berkeley Unic papir klientservermodellen , hvor tidsserveren (dæmonen) afstemmer hver maskine med jævne mellemrum for at spørge, hvad klokken er der. Baseret på svarene beregner den meddelelsernes rundturstid, gennemsnit den aktuelle tid med uvidenhed om eventuelle afvigelser i tidsværdier og “beder alle andre maskiner om at fremme deres ure til den nye tid eller sænke deres ure, indtil der er opnået en bestemt reduktion” .

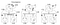
logiske ure

lad os tage et skridt tilbage og genoverveje vores base for synkroniserede tidsstempler. I det foregående afsnit tildeler vi konkrete værdier til alle deltagende maskiners ure, fremover kan de blive enige om en global tidslinje, hvor begivenheder sker under udførelsen af systemet. Det, der virkelig betyder noget i hele tidslinjen, er imidlertid den rækkefølge, hvor relaterede begivenheder forekommer. For eksempel, hvis en eller anden måde behøver vi kun at vide En begivenhed sker, før tilfælde B, det betyder ikke noget, hvis Tₐ = 2, Tᵦ = 6 eller Tₐ = 4, Tᵦ = 10, så længe Tₐ < Tᵦ. Dette skifter vores opmærksomhed mod logiske ure, hvor synkronisering er påvirket af Leslie Lamports definition af “sker-før” – forhold .

Lamports logiske ure

i hans fænomenale papirtid fra 1978, Ure og bestilling af begivenheder i et distribueret System definerede Lamport forholdet” sker før “-forholdet” Kris ” som følger:

1. Hvis A og b er begivenheder i samme proces, og A kommer før b, så er en kur b.

2. Hvis A er afsendelsen af en meddelelse ved en proces, og b er modtagelsen af den samme meddelelse ved en anden proces, så er en kur b.

3. Hvis A B og b C, så A c c.

hvis der forekommer begivenheder i forskellige processer, der ikke udveksler meddelelser, er hverken y eller y y sandt, Y og y siges at være samtidige. Givet en C-funktion, der tildeler en tidsværdi C(A) for en begivenhed, som alle processer er enige om, hvis A og b er begivenheder inden for den samme proces, og a forekommer før b, C(a) < C (b)*. Tilsvarende, hvis a er Afsendelse af en meddelelse ved en proces, og b er modtagelse af denne meddelelse ved en anden proces, C(A) < C(b) **.

lad os nu se på den algoritme, som Lamport foreslog for at tildele tider til begivenheder. Overvej følgende eksempel med en klynge af 3 processer A, B, C:

disse 3 processers ure fungerer på deres egen timing og er oprindeligt ude af synkronisering. Hvert ur kan implementeres med en simpel programmel tæller, forøges med en bestemt værdi hver T tidsenheder. Proces: 1 for a, 5 for B og 2 For C.

på tid 1 sender a besked m1 til B. på ankomsttidspunktet læser uret ved B 10 i sit interne ur. Da meddelelsen er sendt, blev tidsstemplet med tid 1, er værdien 10 I proces B bestemt mulig (Vi kan udlede, at det tog 9 flåter at ankomme til B fra A).

overvej nu besked m2. Det forlader B på 15 og ankommer til C på 8. Denne urværdi ved C er klart umulig, da tiden ikke kan gå baglæns. Fra * * og det faktum, at m2 forlader ved 15, skal den ankomme til 16 eller senere. Derfor er vi nødt til at opdatere den aktuelle tidsværdi ved C for at være større end 15 (Vi tilføjer +1 til tiden for enkelhed). Med andre ord, når en meddelelse ankommer, og modtagerens ur viser en værdi, der går forud for tidsstemplet, der angiver meddelelsesafgangen, videresender modtageren sit ur til at være en tidsenhed mere end afgangstiden. I figur 6 ser vi, at m2 nu korrigerer urværdien ved C til 16. Tilsvarende kommer m3 og m4 til henholdsvis 30 og 36.

fra ovenstående eksempel formulerer Maarten van Steen et al Lamports algoritme som følger:

1. Før du udfører en begivenhed (dvs.sender en besked over netværket, …), p – kringler C-kringler: C-kringler < – C-kringler + 1.

2. Når proces P-kursen sender besked m for at behandle Pj, indstiller den m ‘ s tidsstempel ts(m) lig med C-kursen efter at have udført det foregående trin.

3. Efter modtagelse af en meddelelse m justerer process Pj sin egen lokale tæller som Cj <- maks{CJ, ts(m)} hvorefter den derefter udfører det første trin og leverer meddelelsen til applikationen.

Vektorure

husk tilbage til Lamports definition af “sker-før” forhold, hvis der er to begivenheder A og b sådan, at a forekommer før b, så er a også placeret i den rækkefølge før b, Det vil sige C(A) < C(B). Dette indebærer imidlertid ikke omvendt årsagssammenhæng, da vi ikke kan udlede, at a går før b blot ved at sammenligne værdierne C(A) og C(b) (beviset overlades som en øvelse til læseren).

for at udlede mere information om bestilling af begivenheder baseret på deres tidsstempel foreslås Vektorure, en mere avanceret version af Lamports logiske ur. For hver proces P-Krut af systemet opretholder algoritmen en vektor VC-Krut med følgende attributter:

1. VC KURST: lokal logisk ur på P Kurst, eller antallet af begivenheder, der har fundet sted før den aktuelle tidsstempel.

2. Hvis VC-K = k, ved P-K, AT K-begivenheder har fundet sted på Pj.

algoritmen for Vektorure går derefter som følger:

1. Før du udfører en begivenhed, registrerer P Kurt, at en ny begivenhed sker i sig selv ved at udføre VC kar <- VC kar + 1.

2. Når P-kursen sender en besked m til Pj, indstiller den tidsstempel ts(m) svarende til VC-kursen efter at have udført det foregående trin.

3. Når meddelelsen m er modtaget, proces Pj opdatere hver k af sin egen vektor ur: VCJ maksimalt { VCJ, ts (m)}. Derefter fortsætter det med at udføre det første trin og leverer beskeden til applikationen.

ved disse trin, når en proces PJ modtager en besked m fra proces P Purpur med tidsstempel ts(m), kender den antallet af begivenheder, der har fundet sted ved P Purpur tilfældigt forud for afsendelsen af m. desuden kender Pj også de begivenheder, der har været kendt af P Purpur om andre processer, før du sender m. (Ja det er sandt, hvis du relaterer denne algoritme til Sladderprotokollen purpur).

forhåbentlig lader forklaringen dig ikke ridse dit hoved for længe. Lad os dykke ned i et eksempel for at mestre konceptet:

i dette eksempel har vi tre processer, der alternativt udveksler meddelelser for at synkronisere deres ure sammen. PFI sender besked m1 på logisk tidspunkt VCFI = (1, 0, 0) (trin 1) til P₂. P₂, efter modtagelse af m1 med tidsstempel ts (m1) = (1, 0, 0), justerer sin logiske tid VC₂ til (1, 1, 0) (trin 3) og sender besked m2 tilbage til PFA med tidsstempel (1, 2, 0) (trin 1). På samme måde accepterer process PFL meddelelsen m2 fra P₂, ændrer dets logiske ur til (2, 2, 0) (trin 3), hvorefter den sender besked m3 til potte at (3, 2, 0). Penti justerer sit ur til (3, 2, 1) (Trin 1), efter at det modtager besked m3 fra Phi. Senere tager det i besked m4, sendt af P₂ at (1, 4, 0), og derved justere sit ur til (3, 4, 2) (trin 3).

baseret på hvordan vi spoler frem de interne ure til synkronisering, går begivenhed a forud for begivenhed b, hvis for alle k, ts(a) liter ts(b), og der er mindst et indeks k’ for hvilke ts(A) < ts(B). Det er ikke svært at se, at (2, 2, 0) går forud for (3, 2, 1), Men (1, 4, 0) og (3, 2, 0) kan være i konflikt med hinanden. Derfor kan vi med vektorure opdage, om der er en kausal afhængighed mellem to begivenheder eller ej.

Tag væk

når det kommer til begrebet tid i distribueret system, er det primære mål at opnå den rigtige rækkefølge af begivenhederne. Begivenheder kan placeres enten i kronologisk rækkefølge med fysiske ure eller i logisk rækkefølge med Lamtports logiske Ure og Vektorure langs udførelsestidslinjen.

Hvad er det næste?

næste i serien vil vi gå over, hvordan tidssynkronisering kan give overraskende enkle svar på nogle klassiske problemer i distribuerede systemer: højst en-meddelelser , cache-konsistens og gensidig udelukkelse .

Leslie Lamport: tid, Ure og bestilling af begivenheder i et distribueret System. 1978.

Barbara Liskov: praktiske anvendelser af synkroniserede ure i distribuerede systemer. 1993.

Maarten van Steen, Andreas S. Tanenbaum: distribuerede systemer. 2017.

Barbara Liskov, Liuba Shrira, John: Effektive at-Most-Once meddelelser baseret på synkroniserede ure. 1991.

Cary G. Gray, David R. Cheriton: lejemål: en effektiv fejltolerant mekanisme til distribueret Fil Cache konsistens. 1989.

Ricardo Gusella, Stefano Satti: nøjagtigheden af Ursynkroniseringen opnået ved TEMPO i Berkeley unik 4.3 BSD. 1989.