Espace métrique complet

En mathématiques, un espace métrique complet est un espace métrique dans lequel chaque séquence de Cauchy est convergente. En d’autres termes, chaque suite de Cauchy dans l’espace métrique tend dans la limite à un point qui est à nouveau un élément de cet espace. Par conséquent, l’espace métrique est, en un sens, “complet.”

• 1 Définition formelle
• 2 Exemples
• 3 Complétion
  • 3.1 Exemples
• 4 Espace topologiquement complet
• 5 Voir aussi

Définition formelle

Soit X un espace métrique avec la métrique d. Alors X est complet si pour chaque séquence de Cauchy 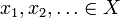il existe un élément 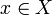tel que .

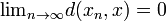Exemples

• Les nombres réels R, et plus généralement les espaces euclidiens de dimension finie, avec la métrique usuelle sont complets.
• Tout espace métrique compact est séquentiellement compact et donc complet. L’inverse ne tient pas: par exemple, R est complet mais pas compact.
• Dans un espace avec la métrique discrète, les seules séquences de Cauchy sont celles qui sont constantes à partir d’un certain point. Par conséquent, tout espace métrique discret est complet. Ainsi, certains espaces métriques complets bornés ne sont pas compacts.
• Les nombres rationnels Q ne sont pas complets. Par exemple, la séquence (xn) définie par x0 = 1, xn + 1 = 1 + 1 / xn est Cauchy, mais ne converge pas en Q. (En R elle converge vers un nombre irrationnel.)

Complétion

Chaque espace métrique X a une complétion 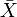qui est un espace métrique complet dans lequel X est intégré isométriquement comme un sous-espace dense. L’achèvement a une propriété universelle.

Exemples

• Les nombres réels R sont l’achèvement des nombres rationnels Q par rapport à la métrique usuelle de la distance absolue.

Espace topologiquement complet

La complétude n’est pas une propriété topologique : il est possible qu’un espace métrique complet soit homéomorphe à un espace métrique qui n’est pas complet. Par exemple, la droite réelle R est homéomorphe à un intervalle ouvert, disons (0,1). Autre exemple : la carte

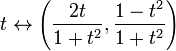
est un homéomorphisme entre l’espace métrique complet R et l’espace incomplet qui est le cercle unitaire dans le plan euclidien avec le point (0, -1) supprimé. Ce dernier espace n’est pas complet car la séquence non-Cauchy correspondent à t = n car n parcourt les entiers positifs est mappée à une séquence de Cauchy non convergente sur le cercle.

Nous pouvons définir un espace topologique à compléter topologiquement métriquement s’il est homéomorphe à un espace métrique complet. Une condition topologique pour cette propriété est que l’espace soit métrisable et un Gδ absolu, c’est-à-dire un Gδ dans chaque espace topologique dans lequel il peut être incorporé (ou simplement Gδ dans son achèvement dans une métrique choisie). En particulier, tous les sous-ensembles ouverts d’espaces euclidiens sont métriquement topologiquement complets.

Voir aussi

• Espace de Banach
• Espace de Hilbert

Certains contenus de cette page sont peut-être déjà apparus sur Citizendium.