Points de vie des Rouages / Wiki réécrit de Toontown

Les rouages ont un certain nombre de points de vie (HP) en fonction de leur niveau. Les rouages de niveau 1 ont la quantité de HP la plus faible, tandis que les rouages de niveau 12 ont la quantité de HP la plus élevée.

Le tableau ci-dessous montre combien de PV chaque niveau de rouage a et quels gags peuvent vaincre le rouage en un seul coup. Certains gags peuvent avoir besoin d’être organiques.

Niveau	Points de vie	Gags à un coup
1	6	Cupcake (6 dégâts) Pot de fleurs (10 dégâts) Verre d’eau (6 dégâts)
2	12	Peau de banane (12 dégâts) Pistolet à gicler (12 dégâts) Sac de sable (18 dégâts)
3	20	Râteau (20 dégâts) Trompe d’éléphant (21 dégâts) Bouteille de Seltz (21 dégâts)
4	30	Tuyau d’incendie (30 dégâts) Enclume (30 dégâts) Billes (35 dommages)
5	42	Gros poids (45 dégâts) Tarte à la crème entière Bio (44 dégâts) Sables mouvants (50 dégâts)
6	56	Coffre-fort (60 dégâts) Trappe (70 dégâts)
7	72	Trappe organique (77 dégâts) Nuage d’orage (80 dégâts)
8	90	Chanteur d’opéra (90 dégâts) Gâteau d’anniversaire (100 dégâts)
9	110	Gâteau d’anniversaire bio (110 dégâts) Geyser bio (115 dommages)
10	132	Gâteau de mariage bio (132 dégâts)
11	156	Piano à queue (170 dégâts) TNT (180 dégâts)
12	200	Chemin de fer organique (214 dégâts)

Formules

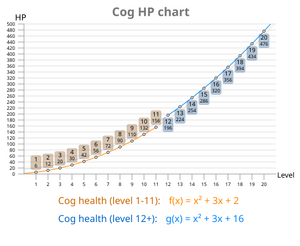
Un graphique montrant la croissance de la santé des rouages par leur niveau. La différence de santé des rouages de niveau 12 peut être observée.

La formule pour la santé d’un rouage peut être soit:

$f(x) = x^{2} + 3x+2$

ou de manière simplifiée:

$f(x) =(x+1) \times(x+2)$

où x est le niveau du rouage et f(x) est une fonction qui renvoie la valeur de santé des rouages.

Par exemple, la formule fonctionne dans la méthode suivante pour les rouages de niveau quatre, qui ont 30 CH :

$f(4)=(4+1)\ temps (4+2)$ ${\ displaystyle f(4) =(5) \ fois (6)}$ ${\ afficher le style f(4)=30}$

La formule ci-dessus s’applique à tous les niveaux de rouage, à l’exception du niveau 12, qui a 200 CH.

Pour récupérer le niveau du rouage à partir d’un HP donné, plutôt que de récupérer le HP à partir du niveau, une formule quadratique peut être utilisée où n est le HP:

$x_{1,2} = {\frac{-3\pm{\sqrt{9-4*(2-n)}}}{2}}$

Par exemple, l’équation sera résolue dans la méthode suivante pour déterminer quel rouage aurait 156 CH:

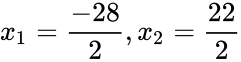
$x_{1,2} = {\frac{-3\pm{\sqrt {9-4*(2-156)}}}{2}}$ ${\ displaystyle x_ {1,2} = {\frac{-3\pm {\sqrt {9-4*-154}}}{2}}}$ ${\ displaystyle x_ {1,2} = {\frac{-3\pm {\sqrt {9+616}}}{2}}}$ ${\ displaystyle x_ {1,2} = {\frac{-3\pm {\sqrt {625}}}{2}}}$ ${\ displaystyle x_ {1,2} = {\frac{-3\pm 25}{2}}}$ ${\ displaystyle x_ {1} = {\frac {-3-25}{2}}, x_{2} = {\frac {-3+25}{2}}}$ ${\ displaystyle x_{1} = {\frac{-28}{2}}, x_{2} = {\frac {22}{2}}}$ ${\ displaystyle x_ {1} = -14, x_{2}=11}$

Puisque f(x) est une fonction d’une parabole et aucune des solutions n’est la valeur minimale de la fonction, il y a deux réponses à l’équation: -14, qui n’est pas un niveau de rouage réel; et 11, qui est un niveau réel.

Bien que cette formule fonctionne pour tous les niveaux de rouage, lorsqu’elle dépasse les niveaux de rouage réguliers, cette formule commence à être inapplicable dans la pratique en raison de nombres complexes. Pour toute valeur de n inférieure à -0,25, cette équation introduit des nombres complexes, qui fonctionnent toujours en théorie mais pas en pratique.

Trivia

Même si les rouages de niveau 12 devraient avoir 182 CH, ils en ont plutôt 200, ce qui représente essentiellement un boost de 10%. Selon la formule, un rouage de 200 CH devrait avoir un niveau d’environ 12,65 (ou environ -15,65, bien que les valeurs négatives ne soient pas compatibles avec les niveaux de rouage).
Selon la formule, le Directeur du marketing d’Embuscade aurait 2 652 CH, étant donné qu’il est de niveau 50.

Points de vie des Rouages

Formules

Trivia

Published by admin

Laisser un commentaire Annuler la réponse