Synchronisation de l’heure dans les Systèmes Distribués

Si vous vous familiarisez avec des sites Web tels que facebook.com ou google.avec, peut-être pas moins d’une fois vous êtes-vous demandé comment ces sites Web peuvent gérer des millions, voire des dizaines de millions de demandes par seconde. Y aura-t-il un seul serveur commercial capable de supporter cette énorme quantité de demandes, de manière à ce que chaque demande puisse être servie en temps opportun pour les utilisateurs finaux?

En approfondissant cette question, nous arrivons au concept de systèmes distribués, un ensemble d’ordinateurs (ou nœuds) indépendants qui apparaissent à ses utilisateurs comme un seul système cohérent. Cette notion de cohérence pour les utilisateurs est claire, car ils pensent avoir affaire à une seule machine gigantesque qui prend la forme de plusieurs processus s’exécutant en parallèle pour traiter des lots de demandes à la fois. Cependant, pour les personnes qui comprennent l’infrastructure du système, les choses ne s’avèrent pas aussi faciles en tant que telles.

Pour des milliers de machines indépendantes fonctionnant simultanément et pouvant couvrir plusieurs fuseaux horaires et continents, certains types de synchronisation ou de coordination doivent être donnés pour que ces machines collaborent efficacement les unes avec les autres (afin qu’elles puissent apparaître comme une seule). Dans ce blog, nous discuterons de la synchronisation du temps et de la manière dont elle atteint la cohérence entre les machines sur l’ordre et la causalité des événements.

Le contenu de ce blog sera organisé comme suit:

1. Synchronisation d’horloge
2. Horloges logiques
3. À emporter
4. Quelle est la prochaine étape?

Horloges physiques

Dans un système centralisé, le temps est sans ambiguïté. Presque tous les ordinateurs ont une “horloge en temps réel” pour suivre l’heure, généralement synchronisée avec un cristal de quartz usiné avec précision. Sur la base de l’oscillation de fréquence bien définie de ce quartz, le système d’exploitation d’un ordinateur peut surveiller avec précision l’heure interne. Même lorsque l’ordinateur est éteint ou s’éteint, le quartz continue de fonctionner grâce à la batterie CMOS, une petite centrale électrique intégrée à la carte mère. Lorsque l’ordinateur se connecte au réseau (Internet), le système d’exploitation contacte ensuite un serveur de minuterie, équipé d’un récepteur UTC ou d’une horloge précise, pour réinitialiser avec précision la minuterie locale à l’aide du protocole de temps réseau, également appelé NTP.

Bien que cette fréquence du quartz cristallin soit raisonnablement stable, il est impossible de garantir que tous les cristaux de différents ordinateurs fonctionneront exactement à la même fréquence. Imaginez un système avec n ordinateurs, dont chaque cristal fonctionne à des vitesses légèrement différentes, provoquant une désynchronisation progressive des horloges et donnant des valeurs différentes lors de la lecture. La différence dans les valeurs de temps causée par cela est appelée inclinaison de l’horloge.

Dans cette circonstance, les choses se sont gâtées pour avoir plusieurs machines séparées spatialement. Si l’utilisation de plusieurs horloges physiques internes est souhaitable, comment les synchroniser avec des horloges du monde réel? Comment les synchronisons-nous les uns avec les autres?

Protocole de temps réseau

Une approche courante pour la synchronisation par paires entre ordinateurs consiste à utiliser le modèle client-serveur, c’est-à-dire à laisser les clients contacter un serveur de temps. Considérons l’exemple suivant avec 2 machines A et B:

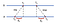
Tout d’abord, A envoie une requête horodatée avec la valeur T₀ à B. B, à l’arrivée du message, enregistre l’heure de réception t₁ à partir de sa propre horloge locale et des réponses avec un message horodaté avec T₂, en récupérant la valeur précédemment enregistrée t₁. Enfin, A, à la réception de la réponse de B, enregistre l’heure d’arrivée T₃. Pour tenir compte du délai de livraison des messages, nous calculons δ₁ = t₁-t₁, Δ₂ = t₁-T₂. Maintenant, un décalage estimé de A par rapport à B est:

Sur la base de θ, on peut soit ralentir l’horloge de A, soit la fixer pour que les deux machines puissent être synchronisées l’une avec l’autre.

Puisque le NTP est applicable par paire, l’horloge de B peut également être ajustée à celle de A. Cependant, il n’est pas sage de régler l’horloge en B si elle est connue pour être plus précise. Pour résoudre ce problème, NTP divise les serveurs en strates, c’est-à-dire les serveurs de classement afin que les horloges des serveurs moins précis avec des rangs plus petits soient synchronisées avec celles des serveurs plus précis avec des rangs plus élevés.

Algorithme de Berkeley

Contrairement aux clients qui contactent périodiquement un serveur de temps pour une synchronisation précise de l’heure, Gusella et Zatti, dans un document Berkeley Unix de 1989, ont proposé le modèle client-serveur dans lequel le serveur de temps (démon) interroge chaque machine périodiquement pour lui demander quelle heure il est là. Sur la base des réponses, il calcule le temps aller-retour des messages, fait la moyenne de l’heure actuelle en ignorant les valeurs de temps aberrantes et “dit à toutes les autres machines d’avancer leurs horloges à la nouvelle heure ou de ralentir leurs horloges jusqu’à ce qu’une réduction spécifiée soit atteinte”.

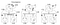
Horloges logiques

Prenons du recul et reconsidérons notre base pour les horodatages synchronisés. Dans la section précédente, nous attribuons des valeurs concrètes aux horloges de toutes les machines participantes, elles peuvent désormais se mettre d’accord sur une chronologie globale à laquelle les événements se produisent pendant l’exécution du système. Cependant, ce qui compte vraiment tout au long de la chronologie, c’est l’ordre dans lequel les événements connexes se produisent. Par exemple, si d’une certaine façon, nous avons seulement besoin de connaître Un événement qui se produit avant l’événement B, il n’a pas d’importance si Tₐ = 2, Tᵦ = 6 ou Tₐ = 4, Tᵦ = 10, aussi longtemps que Tₐ < Tᵦ. Cela déplace notre attention sur le domaine des horloges logiques, où la synchronisation est influencée par la définition de Leslie Lamport de la relation “qui se passe avant”.

Les horloges logiques de Lamport

Dans son document phénoménal de 1978 Time, Clocks, and the Ordering of Events in a Distributed System, Lamport a défini la relation “happens-before” “→” comme suit:

1. Si a et b sont des événements dans le même processus, et a vient avant b, alors a→b.

2. Si a est l’envoi d’un message par un processus et b est la réception du même message par un autre processus, alors a→b.

3. Si a→b et b→c, alors a→c.

Si les événements x, y se produisent dans différents processus qui n’échangent pas de messages, ni x → y ni y → x n’ont la valeur true, x et y sont dits simultanés. Étant donné une fonction C qui attribue une valeur temporelle C(a) à un événement sur lequel tous les processus sont d’accord, si a et b sont des événements dans le même processus et a se produit avant b, C(a) < C(b) *. De même, si a est l’envoi d’un message par un processus et b est la réception de ce message par un autre processus, C(a) < C(b)**.

Examinons maintenant l’algorithme proposé par Lamport pour attribuer des temps aux événements. Considérons l’exemple suivant avec un cluster de 3 processus A, B, C:

Les horloges de ces 3 processus fonctionnent sur leur propre synchronisation et sont initialement désynchronisées. Chaque horloge peut être implémentée avec un compteur logiciel simple, incrémenté d’une valeur spécifique toutes les T unités de temps. Cependant, la valeur d’incrémentation d’une horloge diffère selon le processus : 1 pour A, 5 pour B et 2 pour C.

Au temps 1, A envoie le message m1 à B. Au moment de l’arrivée, l’horloge en B lit 10 dans son horloge interne. Comme le message envoyé a été horodaté avec le temps 1, la valeur 10 dans le processus B est certainement possible (on peut en déduire qu’il a fallu 9 ticks pour arriver à B de A).

Considérons maintenant le message m2. Il part de B à 15 et arrive à C à 8. Cette valeur d’horloge en C est clairement impossible car le temps ne peut pas reculer. De ** et le fait que m2 part à 15, il doit arriver à 16 ou plus tard. Par conséquent, nous devons mettre à jour la valeur de temps actuelle en C pour qu’elle soit supérieure à 15 (nous ajoutons +1 au temps pour plus de simplicité). En d’autres termes, lorsqu’un message arrive et que l’horloge du récepteur affiche une valeur qui précède l’horodatage qui identifie le départ du message, le récepteur avance rapidement son horloge pour être une unité de temps de plus que l’heure de départ. Sur la figure 6, on voit que m2 corrige maintenant la valeur d’horloge en C à 16. De même, m3 et m4 arrivent respectivement à 30 et 36.

À partir de l’exemple ci-dessus, Maarten van Steen et al formulent l’algorithme de Lamport comme suit:

1. Avant d’exécuter un événement (c’est-à-dire envoyer un message sur le réseau, …), pᵢ incrémente cᵢ : cᵢ < – cᵢ +1.

2. Lorsque le processus pᵢ envoie le message m au processus Pj, il définit l’horodatage de m ts(m) égal à cᵢ après avoir exécuté l’étape précédente.

3. A la réception d’un message m, le processus Pj ajuste son propre compteur local en Cj <-max{Cj, ts(m)} après quoi il exécute la première étape et délivre le message à l’application.

Horloges vectorielles

Rappelez-vous la définition de Lamport de la relation “se produit avant”, s’il y a deux événements a et b tels que a se produit avant b, alors a est également positionné dans cet ordre avant b, c’est-à-dire C(a) < C(b). Cependant, cela n’implique pas une causalité inverse, car nous ne pouvons pas en déduire que a précède b simplement en comparant les valeurs de C(a) et C(b) (la preuve est laissée au lecteur).

Afin de dériver plus d’informations sur l’ordre des événements en fonction de leur horodatage, des horloges vectorielles, une version plus avancée de l’horloge logique de Lamport, sont proposées. Pour chaque processus pᵢ du système, l’algorithme maintient un vecteur VCᵢ avec les attributs suivants :

1. VCᵢ : horloge logique locale à pᵢ, ou le nombre d’événements qui se sont produits avant l’horodatage actuel.

2. Si VCᵢ = k, p knows sait que k événements se sont produits à Pj.

L’algorithme des Horloges Vectorielles va alors comme suit:

1. Avant d’exécuter un événement, p records enregistre qu’un nouvel événement se produit sur lui-même en exécutant VCᵢ < -VCᵢ+1.

2. Lorsque pᵢ envoie un message m à Pj, il définit l’horodatage ts(m) égal à VC after après avoir exécuté l’étape précédente.

3. Lorsque le message m est reçu, le processus Pj met à jour chaque k de sa propre horloge vectorielle : VCj ← max {VCj, ts(m)}. Ensuite, il continue d’exécuter la première étape et délivre le message à l’application.

Par ces étapes, lorsqu’un processus Pj reçoit un message m du processus pᵢ avec l’horodatage ts(m), il connaît le nombre d’événements qui se sont produits à p preceded précédés par hasard de l’envoi de m. De plus, Pj connaît également les événements qui ont été connus de pᵢ sur d’autres processus avant d’envoyer m. (Oui c’est vrai, si vous liez cet algorithme au Protocole Potins 🙂).

Espérons que l’explication ne vous laissera pas vous gratter la tête trop longtemps. Plongeons dans un exemple pour maîtriser le concept:

Dans cet exemple, nous avons trois processus p₁, P₂ et p₁ échangeant alternativement des messages pour synchroniser leurs horloges ensemble. P₁ envoie le message m1 à l’instant logique VC₁ =(1, 0, 0) (étape 1) à P₂. P₂, lors de la réception de m1 avec l’horodatage ts (m1) = (1, 0, 0), ajuste son temps logique VC₂ à (1, 1, 0) (étape 3) et renvoie le message m2 à p₁ avec l’horodatage (1, 2, 0) (étape 1). De même, le processus p₁ accepte le message m2 de P₂, modifie son horloge logique en (2, 2, 0) (étape 3), après quoi il envoie le message m3 à p₁ en (3, 2, 0). P₃ ajuste son horloge à (3, 2, 1) (étape 1) après avoir reçu le message m3 de p₁. Plus tard, il reçoit le message m4, envoyé par P₂ à (1, 4, 0), et ajuste ainsi son horloge à (3, 4, 2) (étape 3).

D’après la façon dont nous avançons rapidement les horloges internes pour la synchronisation, l’événement a précède l’événement b si pour tout k, ts(a) ≤ ts(b), et il existe au moins un indice k ‘ pour lequel ts(a) < ts(b). Il n’est pas difficile de voir que (2, 2, 0) précède (3, 2, 1), mais (1, 4, 0) et (3, 2, 0) peuvent entrer en conflit l’un avec l’autre. Par conséquent, avec les horloges vectorielles, nous pouvons détecter s’il existe ou non une dépendance causale entre deux événements quelconques.

À emporter

En ce qui concerne le concept de temps dans un système distribué, l’objectif principal est d’atteindre le bon ordre des événements. Les événements peuvent être positionnés dans l’ordre chronologique avec les Horloges Physiques ou dans l’ordre logique avec les Horloges Logiques et les Horloges Vectorielles de Lamtport le long de la chronologie d’exécution.

Et après ?

Dans la suite de la série, nous verrons comment la synchronisation temporelle peut apporter des réponses étonnamment simples à certains problèmes classiques des systèmes distribués: messages au plus un, cohérence du cache et exclusion mutuelle.

Leslie Lamport: Temps, Horloges et Ordre des événements dans un système distribué. 1978.

Barbara Liskov: Utilisations pratiques des horloges synchronisées dans les systèmes distribués. 1993.

Maarten van Steen, Andrew S. Tanenbaum : Systèmes distribués. 2017.

Barbara Liskov, Liuba Shrira, John Wroclawski: Messages efficaces Au Plus une fois Basés sur des horloges Synchronisées. 1991.

Cary G. Gray, David R. Cheriton : Baux : Un mécanisme Efficace de Tolérance aux pannes pour la Cohérence du Cache de fichiers Distribué. 1989.

Ricardo Gusella, Stefano Zatti: La précision de la Synchronisation de l’horloge Obtenue par TEMPO dans Berkeley UNIX 4.3BSD. 1989.