ベクトル加算

ベクトルは順序付けられたペアまたは数の三重項のいずれかであることをはじめに述べたとき、我々は暗黙的にコンポーネントの観点からベクトルを定義しました。

2次元順序付けられた対(a,b)または3次元三重項(a,b,c)の各エントリは、ベクトルの成分と呼ばれます。 特に指定されない限り、要素は、ベクトルが平面または空間のx、y、および（3Dの場合）z方向に有する単位の数に対応することが通常理解される。 つまり、コンポーネントは、単にベクトルに関連付けられた点の座標と考えることができます。 （ある意味では、ベクトルは点ですが、ベクトルを描画するときは通常、原点から点まで矢印を描画します。)

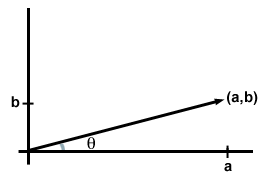
成分を用いたベクトル加算

ユークリッド平面内の二つのベクトルu=(u1,u2)とv=(v1,v2)が与えられると、和は次のように与えられます:

三次元ベクトルu=(u1,u2,u3)およびv=(v1,v2,v3)の場合、式はほぼ同じです:

言い換えれば、ベクトル加算は通常の加算と同じです：成分ごとの成分。

2つの2次元ベクトルを一緒に追加する場合は、別の2次元ベクトルを答えとして取得する必要があることに注意してください。 3次元ベクトルを追加すると、3次元の答えが得られます。 2次元ベクトルと3次元ベクトルは異なるベクトル空間に属し、追加することはできません。 これらの同じ規則は、スカラー乗算を扱っているときに適用されます。