完全距離空間
からKnowino

Jump to:navigation,search
数学において、完備距離空間とは、すべてのコーシー数列が収束する距離空間のことである。 言い換えれば、距離空間内のすべてのコーシー列は、その空間の元である点に限界がある傾向があります。 したがって、距離空間は、ある意味では「完全」である。”
- 1 形式的定義
- 2例
- 3補完
- 3.1例
- 4 位相的完全空間
- 5も参照
形式的定義
xを距離dを持つ距離空間とすると、Xが完全であるとは、すべてのコーシー数列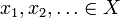 に対して
に対して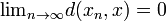 を満たす元
を満たす元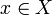 が存在することをいう。
が存在することをいう。
例
- 実数R、より一般的には有限次元ユークリッド空間で、通常の距離を持つものは完全である。
- 任意のコンパクト距離空間は連続的にコンパクトであり、したがって完全である。 逆は成り立たない:例えば、Rは完備であるがコンパクトではない。
- 離散距離を持つ空間では、ある点から一定であるコーシー数列だけが存在する。 したがって、任意の離散距離空間は完全である。 したがって、いくつかの有界完備距離空間はコンパクトではない。
- 有理数Qは完全ではない。 例えば、x0=1,xn+1=1+1/xnで定義される数列(xn)はコーシーであるが、Qには収束しない(Rにおいては無理数に収束する。)
完備
すべての距離空間Xは完備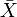 を持ち、これはXが稠密部分空間として等長的に埋め込まれた完全距離空間である。 補完には普遍的なプロパティがあります。
を持ち、これはXが稠密部分空間として等長的に埋め込まれた完全距離空間である。 補完には普遍的なプロパティがあります。
例
- 実数Rは、通常の絶対距離の計量に関する有理数Qの完了です。
位相的に完全な空間
完全性は位相的性質ではない:完全な距離空間が完全でない距離空間に同相であることは可能である。 例えば、実線Rは開区間、例えば(0,1)に同相である。 別の例として、写像
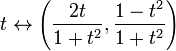
は、完全距離空間Rと、点(0,−1)を削除したユークリッド平面上の単位円である不完全空間との間の同相写像である。 後者の空間は、nが正の整数を通るとき、t=nに対応する非コーシー列が円上の非収束コーシー列に写像されるため、完全ではない。
位相空間が計量位相完備であるとは、それが完備距離空間と同相であることをいう。 この性質の位相的条件は、空間が計量可能であり、絶対G Δ、すなわちそれが埋め込まれることができるすべての位相空間におけるG Δ(または選択された計量におけるその完成におけるG Δ)である。 特に、ユークリッド空間のすべての開部分集合は、計量的に位相的に完全である。
も参照
- バナッハ空間
- ヒルベルト空間
| |
このページの一部のコンテンツは、以前にCitizendiumに掲載されている可能性があります。 |
から取得”http://knowino.org/wiki/Complete_metric_space”