벡터 추가

소개에서 벡터가 정렬 된 쌍 또는 숫자의 삼중 항이라는 것을 언급했을 때 우리는 구성 요소 측면에서 벡터를 암시 적으로 정의했습니다.

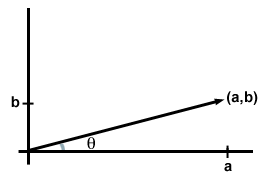
2 차원 정렬 된 쌍(ㅏ,비)또는 3 차원 삼중 항(ㅏ,비,씨)의 각 항목을 벡터의 구성 요소라고합니다. 달리 명시되지 않는 한,일반적으로 엔트리는 벡터가 갖는 단위의 수에 대응한다는 것을 이해한다 엑스,와이,및(3 차원 경우에 대해)지 평면 또는 공간의 방향. 즉,구성 요소를 단순히 벡터와 연결된 점의 좌표로 생각할 수 있습니다. (어떤 의미에서,벡터는 포인트입니다,우리는 벡터를 그릴 때 우리는 일반적으로 점에 원점에서 화살표를 그릴 수 있지만.)

구성 요소를 사용한 벡터 추가

두 벡터가 주어짐 유=(유 1,유 2)및 브이=(브이 1,브이 2)유클리드 평면에서 합은:

3 차원 벡터의 경우 유=(유 1,유 2,유 3)및 브이=(브이 1,브이 2,브이 3),공식은 거의 동일합니다:

즉,벡터 추가는 일반 추가와 같습니다:구성 요소 별 구성 요소.

두 개의 2 차원 벡터를 함께 추가하면 다른 2 차원 벡터를 답으로 가져와야한다는 것을 알 수 있습니다. 3 차원 벡터를 추가하면 3 차원 답이 생성됩니다. 2 차원 및 3 차원 벡터는 다른 벡터 공간에 속하며 추가 할 수 없습니다. 이 같은 규칙은 스칼라 곱셈을 다룰 때 적용됩니다.