전체 메트릭 공간

수학에서 완전한 메트릭 공간은 모든 코시 시퀀스가 수렴하는 메트릭 공간입니다. 즉,메트릭 공간의 모든 코시 시퀀스는 다시 해당 공간의 요소 인 지점으로 제한되는 경향이 있습니다. 따라서 메트릭 공간은 어떤 의미에서”완전합니다.”

• 1 형식적 정의
• 2 예
• 3 완료
  • 3.1 예
• 4 위상 적으로 완전한 공간
• 5 참조

그런 다음 엑스 모든 코시 시퀀스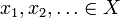에 대해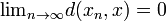과 같은 요소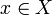가 있으면 완료됩니다.

예

• 실수 아르 자형,보다 일반적으로 유한 차원 유클리드 공간,일반적인 메트릭이 완료되었습니다.
• 모든 소형 메트릭 공간은 순차적으로 컴팩트하므로 완료됩니다. 예를 들어,아르 자형 완전하지만 컴팩트하지 않습니다.
• 이산 메트릭이있는 공간에서 유일한 코시 시퀀스는 어떤 점에서 일정한 시퀀스입니다. 따라서 개별 메트릭 공간이 완료됩니다. 따라서 일부 제한된 전체 메트릭 공간은 컴팩트하지 않습니다.
• 유리수 큐는 완전하지 않다. 예를 들어,시퀀스(엑스 엔)에 의해 정의 엑스 0=1,엑스 엔+1=1+1/엑스 엔 이다 코시,하지만 수렴하지 않습니다 큐.(에 아르 자형 그것은 비합리적인 숫자로 수렴합니다.)

완료

모든 미터법 공간 엑스 완료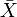이는 완전한 미터법 공간 엑스 등각 적으로 조밀 한 부분 공간으로 포함됩니다. 완성에는 범용 속성이 있습니다.

예

• 실수 아르 자형 유리수의 완성입니다 큐 절대 거리의 일반적인 메트릭에 대해.

위상학적으로 완전한 공간

완전성은 위상학적 속성이 아니다. 예를 들어,실제 라인 아르 자형 이다 동형…에 열린 간격,말하다,(0,1). 또 다른 예:지도

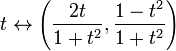
는 완전한 미터법 공간 아르 자형 과 불완전한 공간 이는 유클리드 평면의 단위 원으로 점(0,-1)이 삭제되었습니다. 후자의 공간은 비 코시 시퀀스에 해당하는 완료되지 않습니다 티=엔 으로 엔 양의 정수를 통해 실행 원에 비 수렴 코시 시퀀스에 매핑됩니다.

우리는 토폴로지 공간이 완전한 메트릭 공간과 동형 인 경우 위상 학적으로 완료되도록 정의 할 수 있습니다. 이 속성에 대한 토폴로지 조건은 공간이 측정 가능하고 절대 지 지,즉 지 지 임베디드 될 수있는 모든 토폴로지 공간에서(또는 단지 지 선택한 메트릭에서 완료 될 때).지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지,지 특히,유클리드 공간의 모든 열린 부분 집합은 계량적으로 위상 학적으로 완성됩니다.

참조

• 바나흐 공간
• 힐베르트 공간

이 페이지의 일부 콘텐츠는 이전에 시민권에 등장했을 수 있습니다.