4.1: Kinetisk Energi
Kinetisk Energi I Kollisjoner
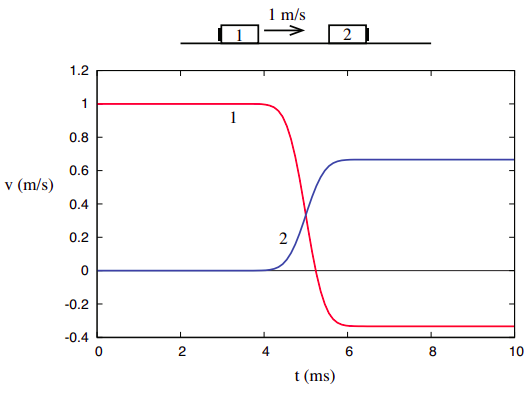
for å få ytterligere innsikt i begrepet kinetisk energi, og hvordan det er forskjellig fra momentum, er det nyttig å se på det i samme innstilling som vi “oppdaget” momentum, nemlig endimensjonale kollisjoner i et isolert system. Hvis vi ser igjen på kollisjonen representert I Figur 3.1.1 I Kapittel 3, gjengitt nedenfor,
\
Merk at 1/18 + 4/9 = 9/18 = 1/2, og så
\
i ord finner vi at i denne kollisjonen er den endelige verdien av den totale kinetiske energien den samme som dens opprinnelige verdi, og så ser det ut til at vi har “oppdaget” en annen bevart mengde (foruten momentum) for dette systemet.
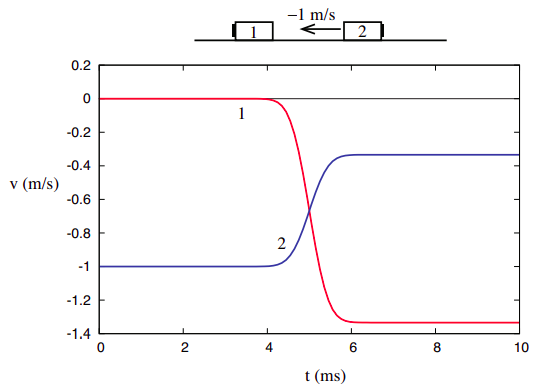
denne troen kan forsterkes hvis vi ser neste på kollisjonen avbildet I Figur 3.1.2 I Kapittel 3, igjen gjengitt nedenfor. Husk jeg påpekte da at vi kan tenke på dette som å være den samme kollisjonen som vist i Figur 3.1.1, bare sett på fra en annen referanseramme(en beveger seg først til høyre ved 1 m / s). Vi vil ha mer å si om hvordan du forvandler mengder fra en referanseramme til en annen ved slutten av kapittelet.
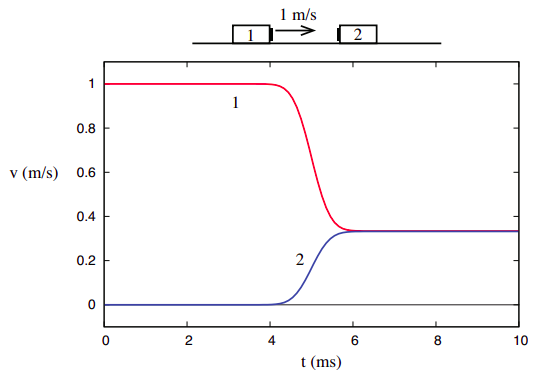
Ting er imidlertid svært forskjellige når vi vurderer det tredje kollisjonseksemplet som vises I Kapittel 3, nemlig den der de to gjenstandene sitter fast sammen etter kollisjonen.
\
hva dette viser, er imidlertid at i motsetning til det totale momentumet i et system, som er helt upåvirket av interne interaksjoner, er den totale kinetiske energien avhengig av detaljene i samspillet, og gir dermed litt informasjon om dens natur. Vi kan da forfine vår studie av kollisjoner for å skille mellom to typer: de der den første kinetiske energien gjenvinnes etter kollisjonen, som vi vil kalle elastisk, og de der det ikke er, som vi kaller uelastisk. Et spesielt tilfelle av uelastisk kollisjon er den som kalles helt uelastisk, hvor de to objektene ender fast sammen, Som I Figur \(\PageIndex{3}\). Som vi skal se senere, er den kinetiske energien” underskudd ” størst i så fall.
jeg har sagt ovenfor at i en elastisk kollisjon blir den kinetiske energien “gjenopprettet”, og jeg foretrekker denne terminologien til “bevart”, fordi faktisk, i motsetning til total momentum, forblir den totale kinetiske energien til et system ikke konstant gjennom samspillet, ikke engang under en elastisk kollisjon. Det enkleste eksempelet for å vise dette ville være en elastisk, frontkollisjon mellom to objekter med lik masse, som beveger seg i samme hastighet mot hverandre. I løpet av kollisjonen blir begge objektene midlertidig stoppet før de reverserer retning og spretter tilbake, og i det øyeblikket er den totale kinetiske energien null.
du kan også undersøke Tallene \(\PageIndex{1}\) og \(\PageIndex{2}\) ovenfor, og beregne, fra grafene, verdien av den totale kinetiske energien under kollisjonen. Du vil se at den faller til et minimum, og kommer deretter tilbake til sin opprinnelige verdi (se Også Figur \(\PageIndex{4}\), senere i dette kapitlet). Konvensjonelt kan vi snakke om kinetisk energi som “bevart” i elastiske kollisjoner, men det er viktig å innse at vi ser på en annen type “bevaring” enn det vi hadde med total momentum, som var konstant før, under og etter samspillet, så lenge systemet forblir isolert.
Elastiske kollisjoner antyder at uansett hva den ultimate naturen til denne tingen vi kaller “energi” kan være, kan det være mulig å lagre det i noen form( i dette tilfellet i løpet av kollisjonen), og deretter gjenopprette det, som kinetisk energi, til slutt. Dette baner vei for innføring av andre typer “energi” foruten kinetisk energi, som vi skal se i et senere kapittel, og muligheten for interconversion å finne sted blant disse typer. For øyeblikket skal vi ganske enkelt si at i en elastisk kollisjon blir en viss mengde kinetisk energi midlertidig lagret som en slags “intern energi”, og etter kollisjonen omdannes denne tilbake til kinetisk energi; mens i en uelastisk kollisjon blir en viss kinetisk energi uigenkallelig omdannet til en “intern energi”, og vi får den aldri tilbake.
siden det som til slutt skjer, avhenger av detaljene og arten av samspillet, vil vi bli ledet til å skille mellom “konservative” interaksjoner, hvor kinetisk energi er reversibelt lagret som en annen form for energi et sted, og “dissipative” interaksjoner, hvor energikonverteringen i det minste delvis er irreversibel. Helt klart, elastiske kollisjoner er forbundet med konservative interaksjoner og uelastiske kollisjoner er forbundet med dissipative interaksjoner. Denne foreløpige klassifiseringen av interaksjoner må vurderes litt mer nøye, men i neste kapittel.