5.8 Visste du at mest nedbør kommer fra kollisjon-koalescens?
5.8 Visste du at det meste av nedbøren kommer fra kollisjons–koalescens?
det finnes to typer prosesser for vekst i nedbørsdråper: varme skyprosesser og kalde skyprosesser. I varme skyer involverer prosessene bare væskedråper. I kalde skyer kan prosessene bare involvere faste partikler, samt blandede faser (både superkjølt væske og is). Noen av de viktigste prosessene involverer kollisjoner mellom dråper, enten de er flytende eller faste.
Kollisjoner
Kollisjoner skjer i både kalde og varme skyer og kan innebære enten væskedråper eller faste partikler eller begge deler.
- Kollisjon-Koalescens: Store flytende dråpe scavenges mindre flytende dråper som den faller.
- Riming: Fallende is samler flytende vann, som fryser på overflaten.
- Fangstkjerne: Stor væskedråpe fanger liten ispartikkel, som fungerer som en iskjerne og får den store dråpen til å fryse. Partikkelen som samles inn kan enten være en iskjerne (I) eller et isstykke, som også er en god iskjerne. I begge tilfeller fryser den superkjølte væskedråpen ved kontakt med INN.
- Aggregering: Fallende snøfnugg scavenges andre snøflak som aggregerer for å lage en større snøfnugg bunt.
for en skyfall i ro er tyngdekraften den eneste eksterne kraften. Når skyfallet begynner å falle, danner luftmotstanden en annen kraft som kalles dra, som er en funksjon av hastigheten.
på mindre enn et sekund når partikkelen en fallhastighet slik at dragkraften nøyaktig balanserer gravitasjonskraften og hastigheten blir konstant. Denne hastigheten kalles terminalhastigheten. Fordi gravitasjonskraften avhenger av volumet av dråpen, går den som kuben av dråperadiusen. I kontrast virker dra på overflaten av dråpen, og så avhenger det av dråpeområdet og går som kvadratet av dråperadiusen (ganger hastigheten). Ved å sette gravitasjons-og dragkreftene lik andre og deretter løse for terminalhastigheten, er det lett å vise at terminalhastigheten skal variere lineært med dråperadius. Målinger bærer dette lineære forholdet ut. For eksempel er terminalhastigheten for et fall i en radius på 50 µ omtrent 0,3 m s–1, mens terminalhastigheten for et fall på 10 ganger større (500 µ radius) er omtrent 4 m s-1, noe som bare øker litt mer enn en faktor-av-10.
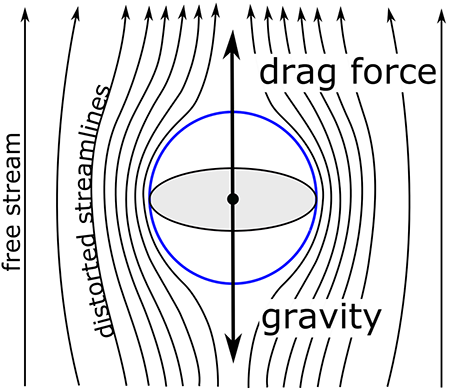
veksten av en skyfall i en nedbør dråpe ved kollisjon-koalescens er gitt av ligningen:
d m L dt = – Området feid ut⋅effektivitet av samlingen⋅hastighet forskjellen⋅flytende vann innhold d m L dt = g ⋅ E c ⋅( v-L − v-s )⋅LWC d m L dt =π ( r L + r ) 2 ⋅ E c ⋅( v-L − v-s )⋅LWC Denne ligningen er ikke gjengi riktig på grunn av en ikke-kompatibel nettleser. Se Tekniske Krav i Retningen for en liste over kompatible nettlesere.
- mL er massen av den store dråpen som faller,
- Ag Er det geometriske tverrsnittsarealet hvor kollisjoner mellom den fallende store dråpen og de mange dråpene nedenfor er mulige,
- Ec er kollisjons–koalescenseffektiviteten (dvs.(mindre dråper kan følge luftstrømlinjer og gå rundt den store dråpen) (se figuren nedenfor),
- vL er hastigheten til den store dråpen og vs er hastigheten til de mindre, langsommere fallende dråpene under,
- OG LWC er det flytende vanninnholdet.
figuren nedenfor gir et godt konseptuelt bilde av kollisjon-koalescens. Kollektorfallet må falle raskere enn den mindre oppsamlede dråpen, slik at de to kan kollidere. Når luften strømlinjeformer bøye seg rundt dråpen, bærer de de mindre dråpene med dem rundt dråpen, og det effektive tverrsnittsarealet blir mindre enn det faktiske tverrsnittsarealet, som bare er tverrsnittsarealet på en disk med en radius som er summen av radiene til den store kollektordråpen og de mindre oppsamlede dråpene. Som dråper blir større, har de for mye treghet til å følge luftstrømlinjene, noe som gjør kollisjonen mer sannsynlig.
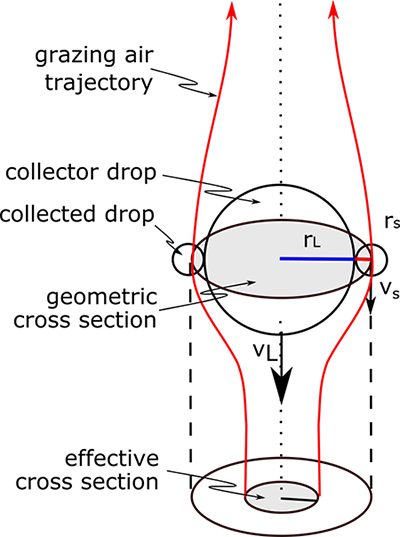
Ec er liten for 10 µ dråper, så ved en tilfeldig prosess blir noen dråper større enn andre og begynner å samle mindre dråper (se figur nedenfor). Ec øker etter hvert som radiusen til den fallende dråpen øker. Når det større fallende fallet får en radius på mer enn 100 µ, er kollisjons–koalescenseffektiviteten veldig bra for alle mindre dråper ned til størrelser på ca.10-20 µ.
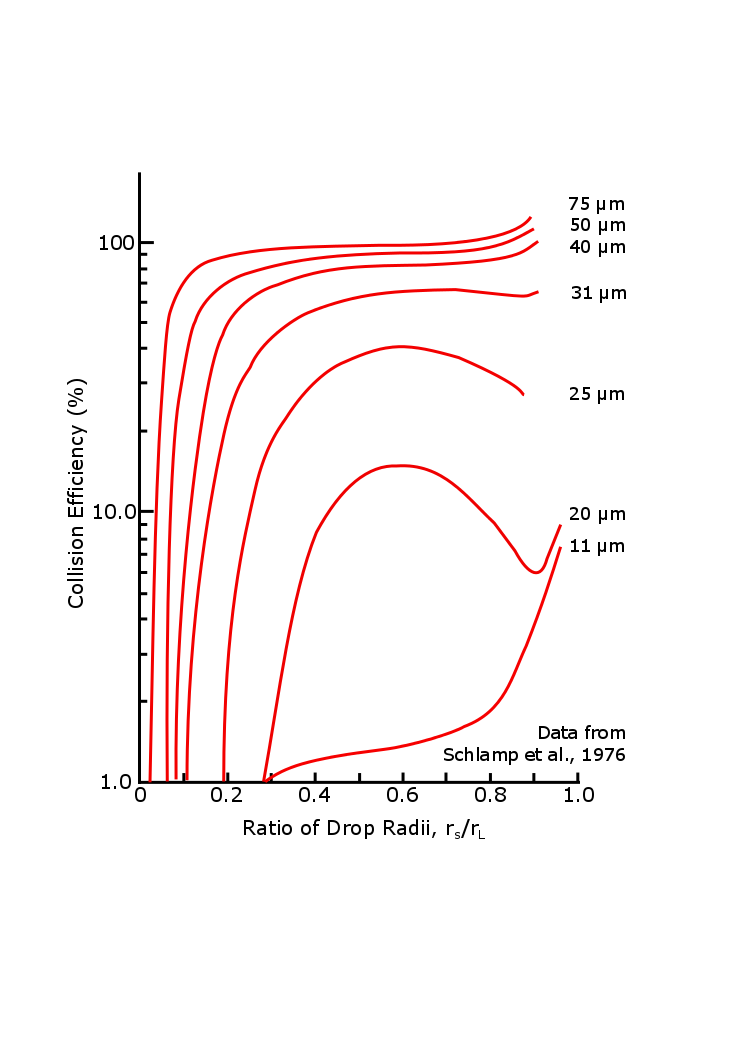
Når en oppsamlingsdråpe har nådd en radius på noen få hundre µ, faller den raskt (vL > > vs) og kollisjons-koalescenseffektiviteten er nær 100%. Ta nå følgende trinn For å omskrive Ligning 5.16: (1) Ec lik 1, (2) vL > > vs, (3) vL = konstant x rL, (4) mL = 4plnrL3 / 3, og (5) løse for drL / dt. Når du tar disse trinnene, kan du vise at drL / dt er proporsjonal med rL. Det er jo jo større dråpen blir, desto raskere vokser den. Separering av variabler (rL og t) og integrering fra rL = 0 ved t = 0 til vilkårlige verdier av rL og t viser at rL øker eksponentielt med tiden:
r d ∝exp (tid) denne ligningen gjengis ikke riktig på grunn av en inkompatibel nettleser. Se Tekniske Krav i Retningen for en liste over kompatible nettlesere.
med konstanten av proporsjonalitet mellom terminalhastigheten og dråperadiusen satt til 0.8 x 10-3 s–1 og LWC = 1 g m-3, det kan påvises at en dråpe kan vokse fra 50 µ til 1000 µ ved kollisjons–koalescens på bare 25 minutter. Så, de aktiverte skydråpene vokser til 10-20 µ ved den langsomme veksten av dampavsetning (kvadratrot av tid). Så når kollisjon-koalescens starter og produserer noen store dråper, kan de vokse eksponentielt med tiden.
Mindre dråper er vanligvis sfæriske. Når disse dråpene kommer til å være over en mm i radius, de blir stadig forvrengt, med en flat bunn på grunn av dra krefter, og de ser litt ut som den øverste halvdelen av en hamburger bun. De kan bli ytterligere forvrengt slik at midten av bun-formen blir presset opp av dragkreftene, slik at dråpen tar på seg en form som ligner en opp ned bolle.
til slutt brytes dråpene opp, enten ved å bli tynne nok i midten at de brytes i stykker eller ved å kollidere med andre dråper så hardt at filamenter eller væskeplater brytes av for å danne andre dråper. Disse prosessene skaper en rekke størrelser av dråper. Dermed regn består av dråper som har et bredt spekter av størrelser. Følgende video (2:50) med tittelen “Hvordan Regndråper Dannes” starter med en forenklet visning av atmosfærens vannsyklus, men viser deretter eksempler på fallende fall, kollisjons–koalescens og sky-dråpe-oppbrudd.
Nå er dette en kjent scene. Solens varme fører vann fra planter, innsjøer og hav for å slå fra en væske til en damp. Høyt oppe i atmosfæren kjøles vanndampen ned og kondenserer fra en gass tilbake til en væske. Det flytende vannet faller deretter tilbake til overflaten i form av regn, snø, is eller hagl. Vann renner ut i bekker innsjøer og hav eller er lagret i bakken eller i snø banen. Dette er vannets kretsløp, og det beskriver vår mest vitale ressurs beveger seg gjennom hele jordsystemet, men som de fleste ting i vår verden når vi ser på de små delene som utgjør hele, kan vi lære mye mer om fenomenet. Ta formen av en enkelt regndråpe. Små dråper vann i atmosfæren er sfæriske i form på grunn av overflatespenningen eller huden til vannmolekylene. Når disse dråpene vokser, blir de tyngre og begynner å falle gjennom luften. Når de faller, kolliderer regndråpen med andre dråper og fortsetter å bli større. Disse større regndråpene faller gjennom luften raskere vindmotstanden på undersiden av dråpen fører til at bunnen av dråpen flater, noe som resulterer i en dråpe som ser ut som en hamburgerbun. Etter hvert som dråpen fortsetter å falle og vokse på et tidspunkt blir den for stor for overflatespenningen å holde den sammen, slik at regndråpen bryter fra hverandre i mindre spirakeldråper. Å undersøke prosessene vi ikke kan se med det blotte øye er ikke noe nytt. Vitenskap og teknologi driver hverandre fremover og fører ofte til innsikt og funn underveis. Med oppfinnelsen av høyhastighetsfotografering så vi endelig de mest grunnleggende elementene i vår våte planet i aksjon. Forstå hvordan en liten regndråpe faller gjennom atmosfæren gjør mer enn avkrefte myten om at en regndråpe Faller som en tåre. Det gjør faktisk en forskjell når det gjelder å måle nedbør spesielt for jordradarer. Jordradarer ser på sidene av regndråpene og anslår deretter de vertikale og horisontale sukkene. En tyngre, flatere dråpe gjør at radarer kan identifisere tyngre nedbør. Faktisk kan de to radarene ombord PÅ gpm-satellitten også måle dråpestørrelser fra rommet, og et mer nøyaktig blikk på regndråper gir oss et mer nøyaktig blikk på hvordan global nedbør utvikler seg.
for riming, fangst nucleation, og aggregering, det er lignende ligninger med begreper som ligner På De i Ligning 5.16 – et område feid ut—en samling effektivitet, den relative hastigheten, og væske eller fast masse konsentrasjonen av de mindre dråper eller is. Disse er vanligvis litt mer kompliserte hvis isen ikke er sfærisk, men konseptene er de samme. Disse prosessene er i stand til å produsere ispartikler som er store nok til å falle, og hvis disse partiklene blir varme når de passerer gjennom den varme delen av skyen, kan de bli til flytende regn. En betydelig del av regn om sommeren kan komme fra iskollisjon-koalescensprosesser over fryselinjen i skyene.