Helse poeng Av Cogs

by Posted on

Tannhjul har et visst antall helse poeng (HP) avhengig av deres nivå. Nivå 1 Tannhjul har den laveste MENGDEN HP, mens Nivå 12 Tannhjul har den høyeste MENGDEN HP.

tabellen nedenfor viser hvor MYE HP HVERT Cog-nivå har og hva gags kan beseire Cog i ett treff. Noen gags må kanskje være organiske.

Nivå Helse poeng One-hit gags
1 6 Cupcake (6 skader)
Blomsterpotte (10 skader)
Glass Vann (6 skader)
2 12 Bananskall (12 skader)
Sprøytepistol (12 skader)
Sandsekk (18 skader)
3 20 Rake (20 skader)
Elefantstamme (21 skader)
Seltzer Flaske (21 skader)
4 30 Brannslange (30 skader)
Ambolt (30 skader)
Klinkekuler (35 skade)
5 42 Stor Vekt (45 skader)
Organisk Hele Bløtkake (44 skader)
Kvikksand (50 skader)
6 56 Sikker (60 skader)
Lemmen (70 skader)
7 72 Organisk Lemmen (77 skade)
Storm Sky (80 skade)
8 90 Operasanger (90 skader)
Bursdagskake (100 skader)
9 110 Organisk Bursdagskake (110 skader)
Organisk Geyser (115 skade)
10 132 Organisk Bryllupskake (132 skade)
11 156 Flygel (170 skader)
TNT (180 skader)
12 200 Organisk Jernbane (214 skade)

Formler

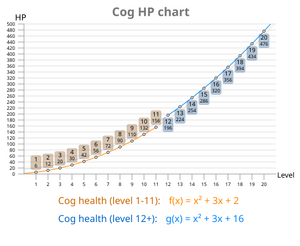
en graf som viser helseveksten Av Tannhjul etter deres nivå. Forskjellen i helse på Nivå 12 Tannhjul kan ses.

formelen for En Tannhelse kan enten være:

{\displaystyle f (x) = x^{2} + 3x + 2}

eller på en forenklet måte:

{\displaystyle f (x)=(x+1)\ganger (x+2)}

hvor x er Tannhjulets nivå og f (x) er en funksjon som returnerer helseverdien til Tannhjul.

formelen fungerer for eksempel i følgende metode for Nivå fire Tannhjul, som har 30 HK:

{\displaystyle f(4)=(4+1)\times (4+2)} {\displaystyle f (4)=(5) \ ganger (6)} {\displaystyle f(4)=30}

formelen ovenfor gjelder for Alle Cog nivå unntatt nivå 12, som har 200 HP.

for å hente Tannhjulets nivå fra EN GITT HP, i stedet for å hente HP fra nivået, kan kvadratisk formel brukes der n er HP:

{\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9-4*(2-n)}}}{2}}}

for eksempel vil ligningen løses i følgende metode for å finne ut hvilken Tannhjul som vil ha 156 HP:

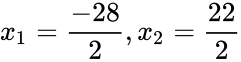
{\displaystyle x_{1,2}={\frac {-3 \ pm {\sqrt {9-4*(2-156)}}}{2}}} {\displaystyle x_{1,2}={\frac {-3 \ pm {\sqrt {9-4*-154}}}{2}}} {\displaystyle x_{1,2}={\frac {-3 \ pm {\sqrt {9+616}}}{2}}} {\displaystyle x_{1,2}={\frac {-3 \ pm {\sqrt {625}}}{2}}} {\displaystyle x_{1,2}={\frac {-3 \ pm 25}{2}}} {\x_{1} = {\frac {-3-25}{2}},x_{2} = {\frac {-3+25}{2}}} {\displaystyle x_{1} = {\frac {-28}{2}}, x_{2} = {\frac {22}{2}}} {\displaystyle x_{1}=-14, x_{2}=11}

siden f (x) er en funksjon av en parabola og ingen av løsningene er funksjonens minimumsverdi, det er to svar for ligningen: -14, som ikke er et ekte Cog-nivå; og 11, som er et ekte nivå.

selv om denne formelen fungerer for Alle Cog nivåer, når du går utover vanlige Cog nivåer, denne formelen begynner å være ubrukelig i praksis på grunn av komplekse tall. For en n-verdi mindre enn -0,25, introduserer denne ligningen komplekse tall, som fortsatt fungerer i teorien, men ikke i praksis.

Trivia

  • selv om nivå 12 Tannhjul skal ha 182 HK, har de i stedet 200, som egentlig er en 10% boost. Ifølge formelen Skal En Tannhjul med 200 HK være omtrent nivå 12,65(eller omtrent -15,65, selv om negative verdier ikke er kompatible med Tannhjul).
  • Ifølge formelen Vil Direktøren For Ambush Marketing ha 2,652 HK, gitt at det er nivå 50.

Published by admin

Legg igjen en kommentar

Din e-postadresse vil ikke bli publisert.