Komplett metrisk plass

i matematikk er et komplett metrisk rom et metrisk rom hvor Hver cauchy-sekvens er konvergent. Med andre ord, hver cauchy-sekvens i det metriske rommet har en tendens til grensen til et punkt som igjen er et element i det rommet. Derfor er det metriske rommet på en måte ” komplett.”

• 1 Formell definisjon
• 2 Eksempler
• 3 Fullføring
  • 3.1 Eksempler
• 4 Topologisk komplett plass
• 5 Se også

Formell definisjon

La X være et metrisk rom med metrisk d. Da Er X fullført hvis for hver cauchy-sekvens 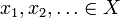er det et element 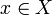slik at .

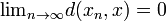Eksempler

• de reelle tallene R, og mer generelt endelige dimensjonale Euklidske rom, med den vanlige metriske er fullført.
• ethvert kompakt metrisk rom er sekvensielt kompakt og dermed komplett. Den omvendte holder ikke: For Eksempel Er R komplett, Men ikke kompakt.
• i et rom med den diskrete metriske er De eneste cauchy-sekvensene de som er konstante fra et tidspunkt på. Derfor er ethvert diskret metrisk rom fullført. Dermed er noen begrensede komplette metriske rom ikke kompakte.
• de rasjonale tallene Q er ikke fullstendige. For eksempel er sekvensen (xn) definert av x0 = 1, xn+1 = 1 + 1 / xn Cauchy, men konvergerer ikke I Q. (I R konvergerer den til et irrasjonelt tall.)

Fullførelse

Hvert metrisk rom x har en fullførelse 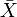som er et komplett metrisk rom Der X er isometrisk innebygd som et tett underrom. Fullførelsen har en universell eiendom.

Eksempler

• de reelle tallene R er fullføringen Av de rasjonelle tallene Q med hensyn Til den vanlige metriske av absolutt avstand.

Topologisk komplett rom

Fullstendighet er ikke en topologisk egenskap: Det er mulig for et komplett metrisk rom å være homeomorphic til et metrisk rom som ikke er fullført. For eksempel er den virkelige linjen R homeomorphic til et åpent intervall, si, (0,1). Et annet eksempel: kartet

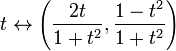
er en homeomorfisme mellom det komplette metriske rommet R og det ufullstendige rommet som er enhetssirkelen i Det Euklidske planet med punktet (0,-1) slettet. Sistnevnte mellomrom er ikke fullført da ikke-Cauchy-sekvensen som svarer til t = n som n går gjennom de positive heltallene, er kartlagt til en ikke-konvergent cauchy-sekvens på sirkelen.

vi kan definere et topologisk rom som skal metrisk topologisk komplett hvis det er homeomorphic til et komplett metrisk rom. En topologisk betingelse for denne egenskapen er at plassen kan metrizes og en absolutt Gδ, det vil si En Gδ i hvert topologisk rom der den kan bygges inn(eller Bare Gδ i ferdigstillelsen i en valgt metrisk). Spesielt er alle åpne undergrupper Av Euklidiske rom metrisk topologisk komplette.

Se også

• Banach plass
• Hilbert plass

Noe innhold på denne siden kan tidligere ha dukket opp på Citizendium.