Tidssynkronisering I Distribuerte Systemer

hvis du finner deg kjent med nettsteder som facebook.com eller google.com, kanskje ikke mindre enn en gang har du lurt på hvordan disse nettstedene kan håndtere millioner eller titalls millioner forespørsler per sekund. Vil det være en enkelt kommersiell server som tåler denne enorme mengden forespørsler, på den måten at hver forespørsel kan serveres rettidig for sluttbrukere?

Når vi Dykker dypere inn i denne saken, kommer vi til begrepet distribuerte systemer, en samling uavhengige datamaskiner (eller noder) som ser ut til brukerne som et enkelt sammenhengende system. Denne oppfatningen av sammenheng for brukere er tydelig, da de tror de har å gjøre med en enkelt humongous maskin som tar form av flere prosesser som kjører parallelt for å håndtere grupper av forespørsler samtidig. Men for folk som forstår systeminfrastruktur, blir det ikke så enkelt som sådan.

for tusenvis av uavhengige maskiner som kjører samtidig som kan strekke seg over flere tidssoner og kontinenter, må noen typer synkronisering eller koordinering gis for at disse maskinene skal samarbeide effektivt med hverandre (slik at de kan vises som en). I denne bloggen vil vi diskutere synkronisering av tid og hvordan det oppnår konsistens blant maskiner på bestilling og årsakssammenheng av hendelser.

innholdet i denne bloggen vil bli organisert som følger:

1. Klokkesynkronisering
2. Logiske klokker
3. Ta bort
4. hva blir det neste?

Fysiske Klokker

i et sentralisert system er tiden entydig. Nesten alle datamaskiner har en “sanntidsklokke” for å holde styr på tiden, vanligvis synkronisert med en nøyaktig maskinert kvartskrystall. Basert på den veldefinerte frekvensoscillasjonen av dette kvarts, kan en datamaskins OS nøyaktig overvåke den interne tiden. Selv når datamaskinen er slått av eller går tom, fortsetter kvarts å krysse på GRUNN AV cmos-batteriet, et lite kraftverk integrert i hovedkortet. NÅR datamaskinen kobles til nettverket (Internett), kontakter OS DERETTER en timerserver, som er utstyrt med EN UTC-mottaker eller en nøyaktig klokke, for å tilbakestille den lokale timeren nøyaktig ved Hjelp Av Network Time Protocol, også kalt NTP.

selv om denne frekvensen av krystallkvarts er rimelig stabil, er det umulig å garantere at alle krystallene i forskjellige datamaskiner vil fungere på nøyaktig samme frekvens. Tenk deg et system med n-datamaskiner, hvis hver krystall kjører på litt forskjellige priser, noe som gjør at klokkene gradvis kommer ut av synkronisering og gir forskjellige verdier når de leses ut. Forskjellen i tidsverdiene forårsaket av dette kalles klokkeforskyvning.

under denne omstendigheten ble det rotete for å ha flere romlig adskilte maskiner. Hvis bruken av flere interne fysiske klokker er ønskelig, hvordan synkroniserer vi dem med virkelige klokker? Hvordan synkroniserer vi dem med hverandre?

Network Time Protocol

en felles tilnærming for parvis synkronisering mellom datamaskiner er ved bruk av klient-servermodellen, dvs. la klienter kontakte en tidsserver. La oss vurdere følgende eksempel med 2 maskiner A og B:

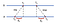
Først sender A en forespørsel timestamped med verdi Tq Til B. B, som meldingen kommer, registrerer tidspunktet for mottak T ^ fra sin egen lokale klokke og svar med en melding timestamped Med T₂, piggybacking den tidligere registrerte verdien T^. Til slutt, a, ved mottak av responsen Fra B, registrerer ankomsttid T⁰. For å redegjøre for tidsforsinkelsen med å levere meldinger, beregner Vi Δ = Lt-Ltq, Δ = Lt-Ltq. Nå er en estimert forskyvning Av a i forhold Til B:

Basert på θ kan Vi enten senke klokken På A eller feste den slik at de to maskinene kan synkroniseres med hverandre.

SIDEN NTP er parvis aktuelt, Kan B klokke justeres til A også. Det er imidlertid uklokt å justere klokken I B hvis det er kjent å være mer nøyaktig. FOR å løse dette problemet, DELER NTP servere i lag, dvs. rangeringsservere slik at klokkene fra mindre nøyaktige servere med mindre ranger vil bli synkronisert til de av de mer nøyaktige med høyere ranger.

Berkeley Algoritme

I motsetning til klienter som jevnlig kontakte en tidsserver for nøyaktig tidssynkronisering, gusella Og Zatti, i 1989 Berkeley Unix papir , foreslo klient-server modell der tidsserveren (daemon) avstemninger hver maskin med jevne mellomrom for å spørre hva klokka er der. Basert på svarene, beregner den rundturstiden for meldingene, gjennomsnitt den nåværende tiden med uvitenhet om eventuelle avvik i tidsverdier, og “forteller alle andre maskiner å fremme sine klokker til den nye tiden eller senke klokkene ned til noen spesifisert reduksjon haw er oppnådd”.

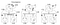
Logiske Klokker

La oss ta et skritt tilbake Og revurdere vår base for synkroniserte tidsstempler. I forrige avsnitt tilordner vi konkrete verdier til alle deltakende maskiners klokker, fremover kan de bli enige om en global tidslinje hvor hendelser skjer under utførelsen av systemet. Men det som virkelig betyr noe gjennom tidslinjen er rekkefølgen der relaterte hendelser oppstår. For eksempel, hvis det er noe vi trenger bare å vite hendelse skjer før En hendelse B, det spiller ingen rolle om Tₐ = 2, Tᵦ = 6 eller Tₐ = 4, Tᵦ = 10, så lenge Tₐ < Tᵦ. Dette skifter vår oppmerksomhet til riket av logiske klokker, hvor synkronisering er påvirket Av Leslie Lamport definisjon av” skjer-før ” forhold .

Lamports Logiske Klokker

I sin fenomenale 1978 paper Time, Clocks, and The Order of Events in A Distributed System , Definerte Lamport” happens-before “relationship” → ” som følger:

1. Hvis a og b er hendelser i samme prosess, og a kommer før b, så er en→b.

2. Hvis a er sending av en melding ved en prosess og b er mottak av den samme meldingen ved en annen prosess, så er en→b.

3. Hvis en→b og b→c, så en→.

hvis hendelser x, y forekommer i forskjellige prosesser som ikke utveksler meldinger, er verken x → y eller y → x sant, x og y sies å være samtidige. Gitt en c-funksjon som tilordner en tidsverdi C(a) For en hendelse som alle prosesser er enige om, hvis a og b er hendelser innenfor samme prosess og a oppstår før b, C(a) < C (b)*. Tilsvarende, hvis a er sending av en melding ved en prosess og b er mottak av meldingen ved en annen prosess, C (a) < C (b) **.

la Oss nå se på algoritmen Som Lamport foreslo for å tildele tider til hendelser. Tenk på følgende eksempel med en klynge av 3 prosesser A, B, C:

disse 3 prosessenes klokker opererer på egen timing og er i utgangspunktet ute av synkronisering. Hver klokke kan implementeres med en enkel programvare teller, økes med en bestemt verdi hver t tid enheter. Verdien som en klokke økes med, varierer imidlertid per prosess: 1 For A, 5 For B og 2 For C.

ved tid 1 sender a melding m1 Til B. på ankomsttidspunktet leser klokken På B 10 i sin interne klokke. Siden meldingen er sendt var timestamped med tid 1, er verdien 10 i prosess B sikkert mulig (vi kan utlede at det tok 9 flått å komme Til B Fra A).

vurder nå melding m2. Den forlater B på 15 og kommer Til C på 8. Denne klokkeverdien Ved C er tydelig umulig siden tiden ikke kan gå bakover. Fra ** og det faktum at m2 forlater 15, må det komme til 16 eller senere. Derfor må vi oppdatere gjeldende tidsverdi Ved C for å være større enn 15 (vi legger til +1 til tiden for enkelhet). Med andre ord, når en melding kommer og mottakerens klokke viser en verdi som går foran tidsstempelet som peikt meldingen avgang, mottakeren raskt fremover sin klokke til å være en tidsenhet mer enn avgangstiden. I figur 6 ser vi at m2 nå korrigerer klokkeverdien Ved C til 16. På samme måte kommer m3 og m4 til henholdsvis 30 og 36.

Fra eksemplet ovenfor formulerer Maarten van Steen et al Lamports algoritme som følger:

1. Før du utfører en hendelse (dvs.sender en melding over nettverket, …), øker Pᵢ Cᵢ: Cᵢ < – Cᵢ + 1.

2. Når prosess Pᵢ sender melding m til prosess Pj, setter den m ‘ s tidsstempel ts (m) lik Cᵢ Etter å ha utført det forrige trinnet.

3. Ved mottak av en melding m, justerer process Pj sin egen lokale teller Som Cj <- max{Cj, ts(m)}, hvorpå den deretter utfører det første trinnet og leverer meldingen til søknaden.

Vektorklokker

Husk Tilbake Til Lamports definisjon av “skjer-før” – forhold, Hvis det er to hendelser a og b slik at a oppstår før b, så er a også plassert i den rekkefølgen før b, det Vil Si C(a) < C(b). Dette innebærer imidlertid ikke omvendt årsakssammenheng, siden vi ikke kan utlede at a går foran b bare ved å sammenligne verdiene Til C (a) og C (b) (beviset er igjen som en øvelse til leseren).

For å utlede mer informasjon om bestilling av hendelser basert på deres tidsstempel, Foreslås Vector Clocks, en mer avansert versjon Av Lamports Logiske Klokke. For hver Prosess Pᵢ av systemet opprettholder algoritmen en vektor VCᵢ med følgende egenskaper:

1. VCᵢ: lokal logisk klokke På Pᵢ, eller antall hendelser som har skjedd før dagens tidsstempel.

2. Hvis VCᵢ = k, vet Pᵢ at k-hendelser har oppstått hos Pj.

algoritmen Til Vektorklokker går da som følger:

1. Før du utfører et arrangement, registrerer Pᵢ en ny begivenhet i seg selv ved å utføre VCᵢ <- VCᵢ + 1.

2. Når Pᵢ sender en melding m Til Pj, setter den tidsstempel ts (m) lik VCᵢ etter å ha utført det forrige trinnet.

3. Når meldingen m er mottatt, behandle Pj oppdatere hver k av sin egen vektor klokke: VCj ← max { VCj, ts (m)}. Deretter fortsetter den å utføre det første trinnet og leverer meldingen til programmet.

ved disse trinnene, når en prosess Pj mottar en melding m fra prosess Pᵢ med tidsstempel ts(m), vet den antall hendelser som har skjedd ved Pᵢ før sending av m. Videre vet Pj også om hendelser Som Har Vært Kjent For Pᵢ om andre prosesser før sending m. (ja det er sant, Hvis du knytter denne algoritmen til Sladderprotokollen 🙂).

Forhåpentligvis vil forklaringen ikke la deg skrape hodet for lenge. La oss dykke inn i et eksempel for å mestre konseptet:

i dette eksemplet har vi tre prosesser Pl, P₂, og Pitius alternativt utveksle meldinger for å synkronisere sine klokker sammen. P ^ sender melding m1 ved logisk tid VC ^ = (1, 0, 0) (trinn 1) Til P₂. P₂, ved mottak av m1 med tidsstempel ts (m1) = (1, 0, 0), justerer sin logiske TID VC₂ til (1, 1, 0) (trinn 3) og sender melding m2 tilbake Til P ^ med tidsstempel (1, 2, 0) (trinn 1). På samme måte aksepterer prosess-Pc-en meldingen m2 fra P₂, endrer den logiske klokken til (2, 2, 0) (trinn 3), hvoretter den sender ut melding m3 til P₂ at (3, 2, 0). Pitius justerer klokken til (3, 2, 1) (trinn 1) etter at den mottar melding m3 fra Pl. Senere tar det inn melding m4, sendt Av P₂ ved (1, 4, 0), og justerer dermed klokken til (3, 4, 2) (trinn 3).

basert på hvordan vi spoler frem de interne klokkene for synkronisering, går hendelse a foran hendelse b hvis for alle k, ts (a) ≤ ts (b), og det er minst en indeks k’ for hvilken ts(a) < ts(b). Det er ikke vanskelig å se at (2, 2, 0) går foran (3, 2, 1), men (1, 4, 0) og (3, 2, 0) kan komme i konflikt med hverandre. Derfor, med vektorklokker, kan vi oppdage om det er en årsakssammenheng mellom to hendelser.

Ta bort

når det gjelder begrepet tid i distribuert system, er det primære målet å oppnå riktig rekkefølge av hendelsene. Hendelser kan plasseres enten i kronologisk rekkefølge Med Fysiske Klokker eller i logisk rekkefølge Med Lamtport Logiske Klokker og Vektor Klokker langs utførelsen tidslinjen.

Hva blir det neste?

Neste opp i serien, vil Vi gå over hvordan tidssynkronisering kan gi overraskende enkle svar på noen klassiske problemer i distribuerte systemer: høyst en meldinger, cache konsistens og gjensidig utelukkelse .

Leslie Lamport: Tid, Klokker og Bestilling Av Hendelser i Et Distribuert System. 1978.

Barbara Liskov: Praktisk bruk av synkroniserte klokker i distribuerte systemer. 1993.

Maarten van Steen, Andrew S. Tanenbaum: Distribuerte Systemer. 2017.

Barbara Liskov, Liuba Shrira, John Wroclawski: Effektiv På Det Meste-En Gang Meldinger Basert På Synkroniserte Klokker. 1991.

Cary G. Gray, David R. Cheriton: Leieavtaler: En Effektiv Feiltolerant Mekanisme For Distribuert Filbuffer Konsistens. 1989.

Ricardo Gusella, Stefano Zatti: Nøyaktigheten Av Klokke Synkronisering Oppnås VED TEMPO I Berkeley UNIX 4.3 BSD. 1989.