4.1: kinetische energie

kinetische energie bij botsingen

om meer inzicht te krijgen in het concept van kinetische energie en de manieren waarop het verschilt van momentum, is het nuttig om ernaar te kijken in dezelfde setting waarin we momentum hebben “ontdekt”, namelijk eendimensionale botsingen in een geïsoleerd systeem. Als we nog eens kijken naar de botsing weergegeven in Figuur 3.1.1 van Hoofdstuk 3, hieronder weergegeven,

\

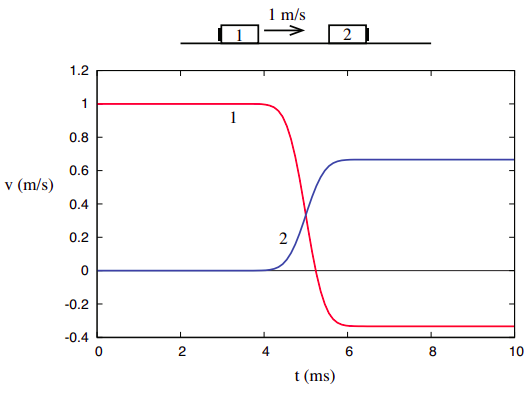
merk op dat 1/18 + 4/9 = 9/18 = 1/2, en dus

\

in woorden, we vinden dat, in deze botsing, de uiteindelijke waarde van de totale kinetische energie is dezelfde als de oorspronkelijke waarde, en dus lijkt het erop dat we hebben “ontdekt” een andere behouden hoeveelheid (naast momentum) voor dit systeem.

dit geloof kan worden versterkt als we vervolgens kijken naar de botsing afgebeeld in Figuur 3.1.2 van Hoofdstuk 3, opnieuw weergegeven hieronder. Herinner me dat ik er toen al op wees dat we dit kunnen zien als echt dezelfde botsing als afgebeeld in Figuur 3.1.1, alleen gekeken vanuit een ander referentiekader (een beweegt aanvankelijk naar rechts bij 1 m/s). We zullen meer te zeggen hebben over de manier waarop de hoeveelheden te transformeren van een referentiekader naar een ander tegen het einde van het hoofdstuk.

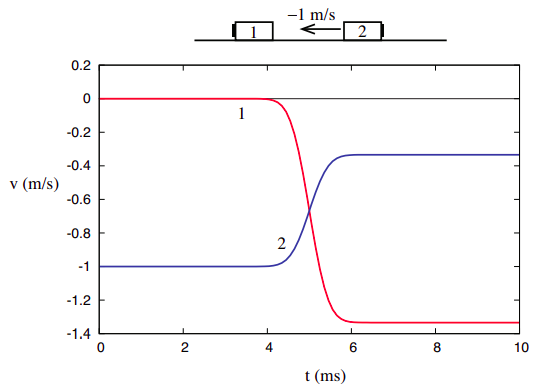
de dingen zijn echter heel anders als we kijken naar het derde botsingsvoorbeeld in hoofdstuk 3, namelijk dat waar de twee objecten aan elkaar vastzitten na de botsing.

\

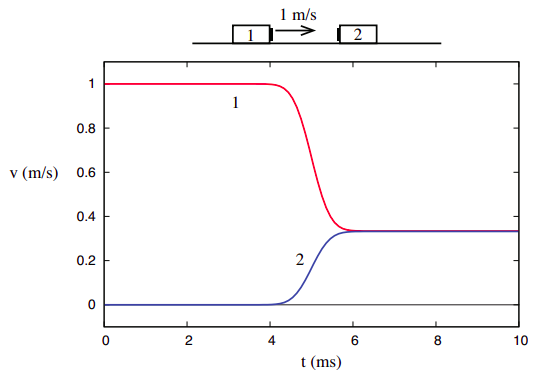
dit toont echter aan dat, in tegenstelling tot het totale momentum van een systeem, dat volledig onaangetast is door interne interacties, de totale kinetische energie afhankelijk is van de details van de interactie, en dus enige informatie over de aard ervan overbrengt. We kunnen dan onze studie van botsingen verfijnen om twee soorten te onderscheiden: die waar de initiële kinetische energie wordt teruggewonnen na de botsing, die we elastisch zullen noemen, en die waar het niet is, die we inelastisch noemen. Een bijzonder geval van inelastische botsingen is die welke totaal inelastisch wordt genoemd, waarbij de twee objecten aan elkaar vast komen te zitten, zoals in Figuur \(\Paginindex{3}\). Zoals we later zullen zien, is het kinetische energie “tekort” in dat geval het grootst.

ik heb hierboven gezegd dat in een elastische botsing de kinetische energie wordt “teruggewonnen”, en ik verkies deze terminologie boven “behouden”, omdat in feite, in tegenstelling tot de totale momentum, de totale kinetische energie van een systeem niet constant blijft gedurende de interactie, zelfs niet tijdens een elastische botsing. Het eenvoudigste voorbeeld om dit te laten zien is een elastische frontale botsing tussen twee voorwerpen van gelijke massa, die met dezelfde snelheid naar elkaar toe bewegen. In de loop van de botsing worden beide objecten tijdelijk tot stilstand gebracht voordat ze omkeren en weerkaatsen, en op dat moment is de totale kinetische energie nul.

u kunt ook bovenstaande figuren \(\Pagindex{1}\) en \(\Pagindex{2}\) onderzoeken en uit de grafieken de waarde berekenen van de totale kinetische energie tijdens de botsing. Je zult zien dat het tot een minimum daalt, en dan terug komt naar zijn beginwaarde (zie ook figuur \(\Paginindex{4}\), later in dit hoofdstuk). Conventioneel kunnen we spreken van kinetische energie als “behouden” in elastische botsingen, maar het is belangrijk om te beseffen dat we kijken naar een ander soort “behoud” dan wat we hadden met de totale momentum, die constant was voor, tijdens en na de interactie, zolang het systeem geïsoleerd bleef.

elastische botsingen suggereren dat, ongeacht de uiteindelijke aard van dit ding dat we “energie” noemen, het mogelijk kan zijn om het op te slaan in een bepaalde vorm (in dit geval, tijdens de botsing), en vervolgens terug te winnen, als kinetische energie, uiteindelijk. Dit effent de weg voor de introductie van andere soorten “energie” naast kinetische energie, zoals we in een later hoofdstuk zullen zien, en de mogelijkheid van interconversie tussen deze soorten. Voor het moment zullen we gewoon zeggen dat in een elastische botsing een bepaalde hoeveelheid kinetische energie tijdelijk wordt opgeslagen als een soort “interne energie”, en na de botsing wordt dit weer omgezet in kinetische energie; terwijl, in een inelastische botsing, een bepaalde hoeveelheid kinetische energie onherroepelijk wordt omgezet in een soort “interne energie”, en we krijgen het nooit terug.

aangezien wat er uiteindelijk gebeurt afhangt van de details en de aard van de interactie, zullen we een onderscheid maken tussen “conservatieve” interacties, waarbij kinetische energie omkeerbaar wordt opgeslagen als een andere vorm van energie ergens, en “dissipatieve” interacties, waarbij de energieconversie ten minste gedeeltelijk onomkeerbaar is. Het is duidelijk dat elastische botsingen worden geassocieerd met conservatieve interacties en inelastische botsingen worden geassocieerd met dissipatieve interacties. Deze voorlopige classificatie van interacties zal echter wat zorgvuldiger moeten worden herzien in het volgende hoofdstuk.