gezondheidspunten van Cogs

by Posted on

Cogs hebben een bepaald aantal gezondheidspunten (HP) afhankelijk van hun niveau. Niveau 1 Cogs hebben de laagste hoeveelheid HP, terwijl niveau 12 Cogs hebben de hoogste hoeveelheid HP.

de tabel hieronder toont hoeveel HP elk Cog-niveau heeft en welke gags het Cog in één treffer kunnen verslaan. Sommige gags moeten biologisch zijn.

Niveau Gezondheid Een one-hit grappen
1 6 Cupcake (6 schade)
Flower Pot (10 schade)
Glas Water (6 schade)
2 12 Banana Peel (12 schade)
waterpistool (12 schade)
Sandbag (18 schade)
3 20 Rake (20 schade)
Elephant Trunk (21 schade)
Seltzer Fles (21 schade)
4 30 Vuur-Slang (30 schade)
Aambeeld (30 schade)
Knikkers (35 schade)
5 42 Grote Gewicht (45 schade)
Organisch Geheel Cream Pie (44 schade)
Drijfzand (50 schade)
6 56 Kluisje (60 schade)
Luik (70 schade)
7 72 Biologische Luik (77 schade)
Storm Cloud (80 schade)
8 90 Opera Zanger (90 schade)
verjaardagstaart (100 schade)
9 110 Biologische verjaardagstaart (110 schade)
Biologische Geiser (115 schade)
10 132 Biologische bruidstaart (132 schade)
11 156 Grand Piano (170 schade)
TNT (180 schade)
12 200 Biologische Spoorlijn (214 schade)

Formules

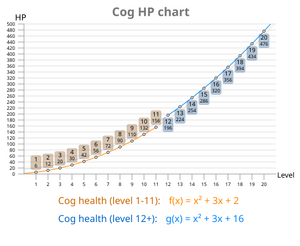
Een grafiek die de gezondheid van de groei van de Tanden door hun niveau. Het verschil in gezondheid van Niveau 12 tandwielen kan worden gezien.

de formule voor de gezondheid van een tandwiel kan ofwel zijn:

{\displaystyle f (x)=x^{2}+3x + 2}

of op een vereenvoudigde manier:

{\displaystyle f (x)=(x+1)\times (x)+2)}

waarbij x het niveau van de tandwielen is en f (x) een functie is die de gezondheidswaarde van tandwielen retourneert.

bijvoorbeeld, de formule werkt in de volgende methode voor niveau vier tandwielen, die 30 pk hebben:

{\displaystyle f(4)=(4+1)\tijden (4+2)} {\displaystyle f (4)=(5) \ times (6)} {\displaystyle f(4)=30}

de bovenstaande formule is van toepassing op elk Cog-niveau, behalve niveau 12, dat 200 pk heeft.

om het Cog-niveau uit een gegeven HP te halen, in plaats van de HP uit het niveau te halen, kan de kwadratische formule worden gebruikt waarbij n de HP is:

{\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9-4*(2-N)}}}{2}}}

bijvoorbeeld, de vergelijking zal worden opgelost in de volgende methode om erachter te komen welke tandwiel 156 pk zou hebben:

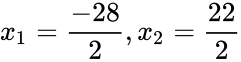
{\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9-4*(2-156)}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9-4*-154}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9+616}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {625}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm 25}{2}}} {\displaystyle x_{1}={\frac {-3-25}{2}},x_{2}={\frac {-3+25}{2}}} {\displaystyle x_{1}={\frac {-28}{2}},x_{2}={\frac {22}{2}}} {\displaystyle x_{1}=-14,x_{2}=11}

Aangezien f(x) is een functie van een parabool en geen van de oplossingen zijn de minimale waarde van de functie, er zijn twee antwoorden voor de vergelijking: -14, dat is geen echt Tandwielniveau; en 11, dat is een echt niveau.

hoewel deze formule voor alle Cog-niveaus werkt, is deze formule in de praktijk niet meer toepasbaar vanwege complexe getallen. Voor elke n-waarde kleiner dan -0,25 introduceert deze vergelijking complexe getallen, die nog steeds in theorie maar niet in de praktijk werken.

Trivia

  • hoewel niveau 12 tandwielen 182 pk zouden moeten hebben, hebben ze in plaats daarvan 200, wat in wezen een boost van 10% is. Volgens de formule moet een radertje met 200 pk ongeveer niveau 12,65 zijn (of ongeveer -15,65, hoewel negatieve waarden niet compatibel zijn met Raderniveaus).
  • volgens de formule zou de directeur van Ambush Marketing 2.652 pk hebben, aangezien het niveau 50 is.

Published by admin

Geef een antwoord

Het e-mailadres wordt niet gepubliceerd.