optische vezel-optische vezel-communicatie vezel

basistermen

lichtbreking

als een lichtstraal van het ene transparante medium naar het andere overgaat, verandert deze van richting; dit fenomeen wordt lichtbreking genoemd. Hoeveel die lichtstraal zijn richting verandert hangt af van de brekingsindex van de mediums.

brekingsindex

is de lichtsnelheid in vacuüm (afgekort c, c = 299.792).458km / seconde) gedeeld door de lichtsnelheid in een materiaal (afgekort v). Brekingsindex meet hoeveel een materiaal licht breekt. Brekingsindex van een materiaal, afgekort als n, wordt gedefinieerd als

n = c/v

de wet van Snell

in 1621 heeft de Nederlandse natuurkundige Willebrord Snell de relatie afgeleid tussen de verschillende lichthoeken als het van het ene transparante medium naar het andere gaat. Wanneer licht van het ene transparante materiaal naar het andere gaat, buigt het volgens de wet van Snell, die wordt gedefinieerd als:

n1sin(θ1) = n2sin(θ2)

waar:
n1 is de brekingsindex van het medium verlaat het licht
θ1 is het incident hoek tussen de lichtstraal en de normaal (normaal is (90°) op het grensvlak tussen twee materialen)
n2 is de brekingsindex van het materiaal het licht
θ2 is de brekende hoek tussen de lichtstraal en de normaal

Opmerking:

Voor het geval van θ1 = 0° (d.w.z. een straal loodrecht op de interface van) de oplossing is θ2 = 0° ongeacht de waarden van n1 en n2. Dat betekent dat een straal die een medium loodrecht op het oppervlak binnenkomt, nooit gebogen is.

het bovenstaande geldt ook voor licht dat van een dicht (hogere n) naar een minder dicht (lagere n) materiaal gaat; de symmetrie van de wet van Snell laat zien dat dezelfde straalpaden in tegengestelde richting van toepassing zijn.

totale interne reflectie

wanneer een lichtstraal een interface kruist naar een medium met een hogere brekingsindex, buigt deze naar het normale. Omgekeerd, licht reizen kruis een interface van een hogere brekingsindexmedium naar een lagere brekingsindexmedium zal wegbuigen van de normale.

dit heeft een interessante implicatie: onder een bepaalde hoek, bekend als de kritische hoek θc, zal licht dat van een hogere brekingsindexmedium naar een lagere brekingsindexmedium gaat, bij 90° worden gebroken, met andere woorden, langs de interface.

als het licht de interface raakt onder een hoek groter dan deze kritische hoek, zal het helemaal niet door het tweede medium gaan. In plaats daarvan zal alles worden gereflecteerd in het eerste medium, een proces dat bekend staat als totale interne reflectie.

de kritische hoek kan worden berekend aan de hand van de wet van Snell, waarbij een hoek van 90° wordt gemaakt voor de hoek van de gebroken straal θ2. Dit geeft θ1:

Sinds

θ2 = 90°

Dus

sin(θ2) = 1

Dan

θc = θ1 = arcsin(n2/n1)

bijvoorbeeld, met licht proberen te voorschijn te komen uit glas met n1=1.5 in de lucht (n2 =1), de kritische hoek θc is arcsin(1/1.5), of 41.8°.

voor elke invalshoek groter dan de kritische hoek, zal de wet van Snell niet kunnen worden opgelost voor de brekingshoek, omdat het zal aantonen dat de brekingshoek een sinus groter dan 1 heeft, wat niet mogelijk is. In dat geval wordt al het licht volledig gereflecteerd van de interface, volgens de wet van reflectie.

hoe optische vezels werken

optische vezels zijn volledig gebaseerd op het principe van totale interne reflectie. Dit wordt uitgelegd in de volgende afbeelding.

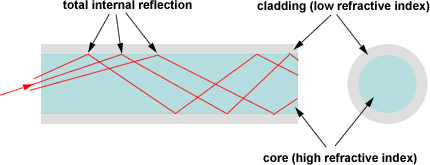
optische vezel is een lange, dunne streng van zeer zuiver glas met een diameter van mensenhaar. Optische vezels worden gerangschikt in bundels genaamd optische kabels en gebruikt om lichtsignalen over lange afstanden te verzenden.

de structuur van een optische vezel

typische optische vezels bestaat uit kern, bekleding en buffercoating.

de kern is het binnenste deel van de vezel, dat licht geleidt. De bekleding omringt de kern volledig. De brekingsindex van de kern is hoger dan die van de bekleding, dus licht in de kern dat de grens met de bekleding raakt onder een hoek ondieper dan kritische hoek zal worden gereflecteerd terug in de kern door totale interne reflectie.

voor de meest voorkomende optische glasvezeltypes, waaronder 1550nm single mode vezels en 850nm of 1300nm multimode vezels, varieert de kerndiameter van 8 ~ 62,5 µm. De meest voorkomende bekledingsdiameter is 125 µm. Het materiaal van buffercoating is meestal zacht of hard plastic zoals acryl, nylon en met een diameter van 250 µm tot 900 µm. Buffercoating biedt mechanische bescherming en buigflexibiliteit voor de vezel.

Optische Vezelmodus

Wat is Vezelmodus?

een optische vezel geleidt lichtgolven in verschillende patronen die modi worden genoemd. Modus beschrijft de verdeling van lichtenergie over de vezel. De precieze patronen hangen af van de golflengte van het uitgezonden licht en van de variatie in brekingsindex die de kern vormt. In essentie creëren de variaties in brekingsindex randvoorwaarden die vorm geven aan hoe lichtgolven door de vezel reizen, zoals de wanden van een tunnel de echo van geluiden binnen beïnvloeden.

we kunnen een kijkje nemen op large-core step-index vezels. Lichtstralen voeren de vezel in een bereik van hoeken, en stralen onder verschillende hoeken kunnen allemaal stabiel reizen over de lengte van de vezel, zolang ze de kern-bekleding interface raken onder een hoek groter dan kritische hoek. Deze stralen zijn verschillende modi.

vezels die meer dan één modus dragen bij een specifieke lichtgolflengte worden multimode-vezels genoemd. Sommige vezels hebben een zeer kleine diameter kern die ze kunnen slechts één modus die reist als een rechte lijn in het centrum van de kern dragen. Deze vezels zijn single mode vezels. Dit wordt geïllustreerd in de volgende afbeelding.

Optische Vezelindexprofiel

Indexprofiel is de verdeling van de brekingsindex over de kern en de bekleding van een vezel. Sommige optische vezels hebben een stapindexprofiel, waarbij de kern één gelijkmatig verdeelde index heeft en de bekleding een lagere gelijkmatig verdeelde index heeft. Andere optische vezel heeft een graded indexprofiel, waarbij brekingsindex geleidelijk varieert als functie van de radiale afstand van het vezelcentrum. Graded-index profielen omvatten power-law index profielen en parabolische index profielen. De volgende figuur toont enkele veel voorkomende soorten indexprofielen voor single mode en multimode vezels.

numerieke apertuur (NA)

Multimode optische vezel zal alleen licht verspreiden dat de vezel binnen een bepaalde kegel binnendringt, bekend als de acceptatiekegel van de vezel. De halve hoek van deze kegel wordt de acceptatiehoek genoemd, θmax. Voor stap-index multimode vezel, wordt de acceptatiehoek alleen bepaald door de indices van breking:

waarbij
n de brekingsindex is van het medium licht dat de vezel binnenkomt
nf is de brekingsindex van de vezelkern
nc is de brekingsindex van de bekleding

modi worden soms gekenmerkt door getallen. Single mode vezels dragen alleen de laagste-orde modus, toegewezen het nummer 0. Multimode vezels dragen ook hogere-orde modi. Het aantal modi dat zich in een vezel kan voortplanten hangt van de numerieke opening van de vezel (of acceptatiehoek) evenals van zijn kerndiameter en de golflengte van het licht af. Voor een stap-index multimode vezel wordt het aantal van deze modi, Nm, benaderd door

waarbij
D de kerndiameter
λ de operationele golflengte
NA de numerieke apertuur (of acceptatiehoek)

Opmerking: Deze formule is slechts een benadering en werkt niet voor vezels die slechts een paar modi dragen.