Vector optelling

toen we in de inleiding vermeldden dat een vector een geordend paar of een triplet getallen is, definieerden we impliciet vectoren in termen van componenten.

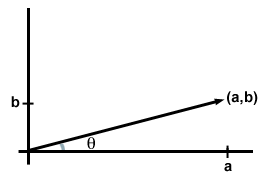
elk item in het 2-dimensionale geordende paar (a, b) of 3-dimensionale triplet (a, b, c) wordt een component van de vector genoemd. Tenzij anders vermeld, wordt normaal gesproken begrepen dat de items overeenkomen met het aantal eenheden dat de vector heeft in de x -, y-en (voor het 3D-geval) z-richtingen van een vlak of ruimte. Met andere woorden, je kunt van de componenten denken als gewoon de coördinaten van het punt geassocieerd met de vector. (In zekere zin is de vector het punt, hoewel als we vectoren tekenen we normaal gesproken een pijl van de oorsprong naar het punt tekenen.)

Vector optelling met behulp van componenten

gegeven twee vectoren u = (U1, u2) en v =(v1, v2) in het Euclidische vlak, wordt de som gegeven door:

Voor drie-dimensionale vectoren u = (u1, u2, u3) en v = (v1, v2, v3), de formule is bijna identiek:

In andere woorden, vector toevoeging is net als gewone toevoeging: component per component.

merk op dat als je twee 2-dimensionale vectoren optelt, je een andere 2-dimensionale vector als antwoord moet krijgen. Toevoeging van 3-dimensionale vectoren zal 3-dimensionale antwoorden opleveren. 2-en 3-dimensionale vectoren behoren tot verschillende vectorruimten en kunnen niet worden toegevoegd. Dezelfde regels gelden wanneer we te maken hebben met scalaire vermenigvuldiging.