volledige metrische ruimte

in de wiskunde is een volledige metrische ruimte een metrische ruimte waarin elke Cauchy-reeks convergent is. Met andere woorden, elke Cauchy-reeks in de metrische ruimte neigt in de limiet naar een punt dat weer een element van die ruimte is. Vandaar dat de metrische ruimte in zekere zin “compleet” is.”

• 1 formele definitie
• 2 Voorbeelden
• 3 voltooiing
  • 3.1 voorbeelden
• 4 topologisch volledige ruimte
• 5 Zie ook

formele definitie

zij X een metrische ruimte met metrisch d. dan is X compleet als er voor elke Cauchy-reeks 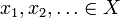een element 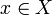is, zodanig dat .

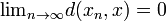voorbeelden

• de reële getallen R, en meer in het algemeen eindig-dimensionale Euclidische ruimten, met de gebruikelijke metriek zijn compleet.
• elke compacte metrische ruimte is sequentieel compact en dus compleet. De converse houdt niet: bijvoorbeeld, R is compleet maar niet compact.
• in een ruimte met de discrete metriek zijn de enige Cauchy-sequenties die vanaf een bepaald punt constant zijn. Vandaar dat elke discrete metrische ruimte compleet is. Sommige begrensde volledige metrische ruimten zijn dus niet compact.
• de rationale getallen Q zijn niet volledig. Bijvoorbeeld, de reeks (xn) gedefinieerd door x0 = 1, xn+1 = 1 + 1/xn is Cauchy, maar convergeert niet in Q. (In R convergeert het naar een irrationeel getal.)

voltooiing

elke metrische ruimte X heeft een voltooiing 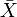wat een volledige metrische ruimte is waarin X isometrisch is ingebed als een dichte subruimte. De voltooiing heeft een universele eigenschap.

voorbeelden

• de reële getallen R zijn de voltooiing van de rationale getallen Q ten opzichte van de gebruikelijke metriek van absolute afstand.

topologisch volledige ruimte

volledigheid is geen topologische eigenschap: Het is mogelijk dat een volledige metrische ruimte homeomorf is met een niet-complete metrische ruimte. Bijvoorbeeld, de reële lijn R is homeomorf met een open interval, laten we zeggen, (0,1). Een ander voorbeeld: de afbeelding

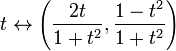
is een homeomorfisme tussen de volledige metrische ruimte R en de onvolledige ruimte die de eenheidscirkel is in het Euclidische vlak met het punt (0,-1) verwijderd. De laatste ruimte is niet compleet omdat de niet-Cauchy-reeks die overeenkomt met t=n als n door de positieve gehele getallen loopt, is toegewezen aan een niet-convergente Cauchy-reeks op de cirkel.

we kunnen een topologische ruimte definiëren die metrisch topologisch compleet is als deze homeomorf is met een volledige metrische ruimte. Een topologische voorwaarde voor deze eigenschap is dat de ruimte metrizeerbaar is en een absolute Gδ, dat wil zeggen een Gδ in elke topologische ruimte waarin het kan worden ingebed (of gewoon Gδ in zijn voltooiing in een gekozen metriek). In het bijzonder zijn alle open deelverzamelingen van Euclidische ruimten metrisch topologisch compleet.

zie ook

• Banachruimte
• Hilbertruimte

sommige inhoud op deze pagina kan eerder zijn verschenen op Citizendium.