spațiu metric complet

în matematică, un spațiu metric complet este un spațiu metric în care fiecare secvență Cauchy este convergentă. Cu alte cuvinte, fiecare secvență Cauchy din spațiul metric tinde în limită la un punct care este din nou un element al acelui spațiu. Prin urmare, spațiul metric este, într-un sens, “complet.”

• 1 definiție formală
• 2 Exemple
• 3 Finalizare
  • 3.1 Exemple
• 4 spațiu complet topologic
• 5 Vezi și

definiție formală

fie X un spațiu metric cu metrica d. atunci X este complet dacă pentru fiecare secvență Cauchy 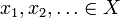există un element 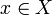astfel încât .

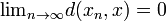Exemple

• numerele reale R și, în general, spațiile euclidiene cu dimensiuni finite, cu metrica obișnuită, sunt complete.
• orice spațiu metric compact este secvențial compact și, prin urmare, complet. Conversa nu este valabilă: de exemplu, R este complet, dar nu compact.
• într-un spațiu cu metrica discretă, singurele secvențe Cauchy sunt cele care sunt constante de la un moment dat. Prin urmare, orice spațiu metric discret este complet. Astfel, unele spații metrice complete delimitate nu sunt compacte.
• numerele raționale Q nu sunt complete. De exemplu, secvența (xn) definită de x0 = 1, xn+1 = 1 + 1/xn este Cauchy, dar nu converge în Q. (În R converge la un număr irațional.)

finalizare

fiecare spațiu metric X are o finalizare 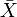care este un spațiu metric complet în care X este încorporat izometric ca un subspațiu dens. Finalizarea are o proprietate universală.

Exemple

• numerele reale R sunt completarea numerelor raționale Q în raport cu metrica obișnuită a distanței absolute.

spațiu complet topologic

completitudinea nu este o proprietate topologică: este posibil ca un spațiu metric complet să fie homeomorf pentru un spațiu metric care nu este complet. De exemplu, linia reală R este homeomorfă la un interval deschis, să zicem, (0,1). Un alt exemplu: harta

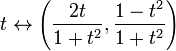
este un homeomorfism între spațiul metric complet R și spațiul incomplet care este cercul unitar din planul euclidian cu punctul (0,-1) șters. Ultimul spațiu nu este complet, deoarece secvența non-Cauchy corespunzătoare t=n pe măsură ce n trece prin numerele întregi pozitive este mapată la o secvență Cauchy neconvergentă pe cerc.

putem defini un spațiu topologic care să fie complet Metric topologic dacă este homeomorf la un spațiu metric complet. O condiție topologică pentru această proprietate este aceea că spațiul să fie metrizabil și un G absolut, adică un G la sută în fiecare spațiu topologic în care poate fi încorporat (sau doar G la sută în completarea sa într-o metrică aleasă). În special, toate subseturile deschise ale spațiilor euclidiene sunt complete Metric topologic.

Vezi și

• spațiul Banach
• spațiul Hilbert

este posibil ca unele conținuturi de pe această pagină să fi apărut anterior pe Citizendium.