4.1: Kinetische Energie
Kinetische Energie bei Kollisionen
Um weitere Einblicke in das Konzept der kinetischen Energie und die Art und Weise zu erhalten, in der sie sich vom Impuls unterscheidet, ist es nützlich, sie in derselben Umgebung zu betrachten, in der wir den Impuls “entdeckt” haben, nämlich eindimensionale Kollisionen in einem isolierten System. Wenn wir uns noch einmal die Kollision ansehen, die in Abbildung 3.1.1 von Kapitel 3 dargestellt ist und unten wiedergegeben ist,
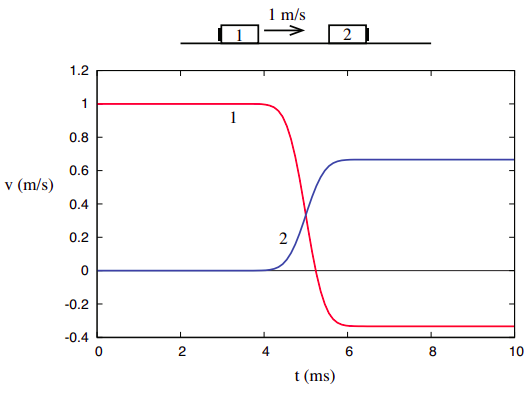
\
Beachten Sie, dass 1/18 + 4/9 = 9/18 = 1/2 und so
\
Mit anderen Worten, wir finden, dass in dieser Kollision der Endwert der gesamten kinetischen Energie der gleiche ist wie sein Anfangswert, und so sieht es so aus, als hätten wir eine andere konservierte Größe (neben dem Impuls) für dieses System “entdeckt”.
Dieser Glaube kann verstärkt werden, wenn wir uns als nächstes die Kollision ansehen, die in Abbildung 3.1.2 von Kapitel 3 dargestellt ist, die unten wiedergegeben ist. Erinnern wir uns, dass ich damals darauf hingewiesen habe, dass wir uns dies als die gleiche Kollision vorstellen können, wie in Abbildung 3.1 dargestellt.1 nur von einem anderen Bezugsrahmen aus betrachtet (einer bewegt sich zunächst mit 1 m/s nach rechts). Wir werden am Ende des Kapitels mehr darüber zu sagen haben, wie Mengen von einem Referenzrahmen in einen anderen umgewandelt werden können.
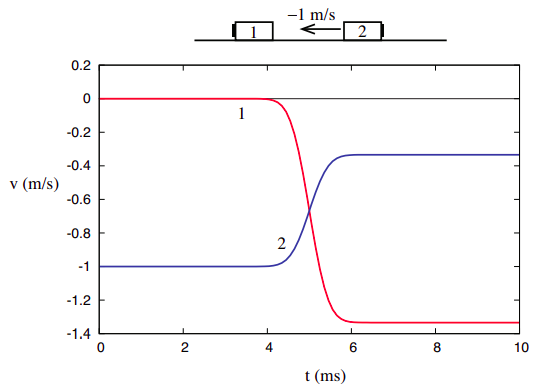
Ganz anders sieht es jedoch beim dritten Kollisionsbeispiel in Kapitel 3 aus, bei dem die beiden Objekte nach der Kollision miteinander verklebt sind.
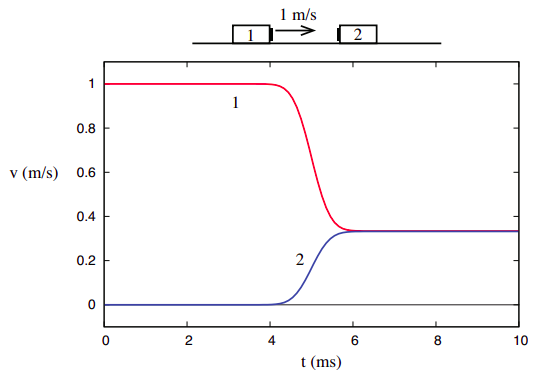
\
Dies zeigt jedoch, dass im Gegensatz zum Gesamtimpuls eines Systems, der von internen Wechselwirkungen völlig unberührt bleibt, die gesamte kinetische Energie von den Details der Wechselwirkung abhängt und somit einige Informationen über seine Natur vermittelt. Wir können dann unsere Kollisionsstudie verfeinern, um zwei Arten zu unterscheiden: diejenigen, bei denen die anfängliche kinetische Energie nach der Kollision zurückgewonnen wird, die wir als elastisch bezeichnen, und diejenigen, bei denen dies nicht der Fall ist, die wir als unelastisch bezeichnen. Ein Sonderfall der unelastischen Kollision ist der als völlig unelastisch bezeichnete Fall, bei dem die beiden Objekte wie in Abbildung \(\pageIndex {3}\) zusammengeklebt werden. Wie wir später sehen werden, ist das “Defizit” der kinetischen Energie in diesem Fall am größten.
Ich habe oben gesagt, dass bei einer elastischen Kollision die kinetische Energie “zurückgewonnen” wird, und ich ziehe diese Terminologie “konserviert” vor, weil die gesamte kinetische Energie eines Systems im Gegensatz zum Gesamtimpuls nicht während der gesamten Wechselwirkung konstant bleibt, nicht einmal während einer elastischen Kollision. Das einfachste Beispiel, um dies zu zeigen, wäre eine elastische Frontalkollision zwischen zwei Objekten gleicher Masse, die sich mit der gleichen Geschwindigkeit aufeinander zu bewegen. Im Verlauf der Kollision werden beide Objekte kurzzeitig zum Stillstand gebracht, bevor sie die Richtung umkehren und zurückprallen, und in diesem Moment ist die gesamte kinetische Energie Null.
Sie können auch die obigen Abbildungen \(\pageIndex{1}\) und \(\pageIndex{2}\) untersuchen und aus den Diagrammen den Wert der gesamten kinetischen Energie während der Kollision berechnen. Sie werden sehen, dass es auf ein Minimum absinkt und dann zu seinem Anfangswert zurückkehrt (siehe auch Abbildung \(\pageIndex{4}\), später in diesem Kapitel). Konventionell können wir von kinetischer Energie als “konserviert” in elastischen Kollisionen sprechen, aber es ist wichtig zu erkennen, dass wir eine andere Art von “Konservierung” betrachten als mit dem Gesamtimpuls, der vor, während und nach der Wechselwirkung konstant war, solange das System isoliert blieb.
Elastische Kollisionen deuten darauf hin, dass, was auch immer die ultimative Natur dieses Dings sein mag, das wir “Energie” nennen, es möglich sein könnte, es in irgendeiner Form zu speichern (in diesem Fall während des Verlaufs der Kollision) und es dann schließlich als kinetische Energie wiederzugewinnen. Dies ebnet den Weg für die Einführung anderer Arten von “Energie” neben der kinetischen Energie, wie wir in einem späteren Kapitel sehen werden, und die Möglichkeit der Umwandlung zwischen diesen Arten. Für den Moment wollen wir einfach sagen, dass bei einer elastischen Kollision eine gewisse Menge kinetischer Energie als eine Art “innere Energie” zwischengespeichert wird und nach der Kollision wieder in kinetische Energie umgewandelt wird; während bei einer unelastischen Kollision eine gewisse Menge kinetischer Energie unwiderruflich in eine “innere Energie” umgewandelt wird und wir sie nie zurückbekommen.
Da alles, was letztendlich geschieht, von den Details und der Art der Wechselwirkung abhängt, werden wir dazu gebracht, zwischen “konservativen” Wechselwirkungen zu unterscheiden, bei denen kinetische Energie reversibel als eine andere Energieform irgendwo gespeichert wird, und “dissipativen” Wechselwirkungen, bei denen die Energieumwandlung zumindest teilweise irreversibel ist. Es ist klar, dass elastische Kollisionen mit konservativen Wechselwirkungen und unelastische Kollisionen mit dissipativen Wechselwirkungen verbunden sind. Diese vorläufige Klassifizierung der Wechselwirkungen muss jedoch im nächsten Kapitel etwas genauer überprüft werden.