Espacio métrico completo

En matemáticas, un espacio métrico completo es un espacio métrico en el que cada secuencia de Cauchy es convergente. En otras palabras, cada secuencia de Cauchy en el espacio métrico tiende en el límite a un punto que es de nuevo un elemento de ese espacio. Por lo tanto, el espacio métrico es, en cierto sentido, “completo.”

• 1 Definición formal
• 2 Ejemplos
• 3 Finalización
  • 3.1 Ejemplos
• 4 Espacio topológicamente completo
• 5 Véase también

Definición formal

Sea X un espacio métrico con métrica d. Entonces X está completo si para cada secuencia de Cauchy 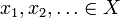hay un elemento 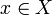tal que .

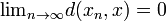Ejemplos

• Los números reales R, y más generalmente los espacios euclidianos de dimensiones finitas, con la métrica habitual, están completos.
• Cualquier espacio métrico compacto es secuencialmente compacto y, por lo tanto, completo. La inversa no se sostiene: por ejemplo, R es completa pero no compacta.
• En un espacio con la métrica discreta, las únicas secuencias de Cauchy son las que son constantes desde algún punto en adelante. Por lo tanto, cualquier espacio métrico discreto está completo. Por lo tanto, algunos espacios métricos completos acotados no son compactos.
• Los números racionales Q no están completos. Por ejemplo, la secuencia (xn) definida por x0 = 1, xn+1 = 1 + 1/xn es Cauchy, pero no converge en Q. (En R converge a un número irracional.)

Terminación

Cada espacio métrico X tiene una terminación 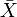que es un espacio métrico completo en el que X está incrustado isométricamente como un subespacio denso. La terminación tiene una propiedad universal.

Ejemplos

• Los números reales R son la terminación de los números racionales Q con respecto a la métrica habitual de distancia absoluta.

Espacio topológicamente completo

La integridad no es una propiedad topológica: es posible que un espacio métrico completo sea homeomorfo a un espacio métrico que no está completo. Por ejemplo, la recta real R es homeomorfa a un intervalo abierto, digamos, (0,1). Otro ejemplo: el mapa

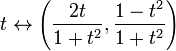
es un homeomorfismo entre el espacio métrico completo R y el espacio incompleto que es el círculo unitario en el plano euclidiano con el punto (0,-1) eliminado. Este último espacio no está completo, ya que la secuencia no-Cauchy correspondiente a t=n, ya que n corre a través de los enteros positivos, se asigna a una secuencia de Cauchy no convergente en el círculo.

Podemos definir que un espacio topológico sea topológicamente completo métricamente si es homeomórfico a un espacio métrico completo. Una condición topológica para esta propiedad es que el espacio sea metrizable y un Gδ absoluto, es decir, un Gδ en cada espacio topológico en el que se puede incrustar (o simplemente Gδ en su terminación en una métrica elegida). En particular, todos los subconjuntos abiertos de espacios euclidianos están topológicamente completos métricamente.

Véase también

• Espacio Banach
• Espacio Hilbert

Parte del contenido de esta página puede haber aparecido anteriormente en Citizendium.