Interpolación Circular: Mecanizado de Trayectorias de Herramientas Circulares
Al trabajar a máquina, las velocidades y los avances adecuados son muy importantes para evitar roturas y maximizar el rendimiento. Las fórmulas tradicionales de fresado de extremos utilizan Material de superficie (SFM) y Carga de virutas (IPT) para calcular las velocidades de Velocidad (RPM) y de Avance (IPM). Estas fórmulas dictan los parámetros de mecanizado correctos para su uso en una trayectoria lineal en la que la línea central de la fresa de extremo se desplaza en línea recta. Dado que no todas las piezas están hechas de superficies planas, las fresas de extremo invariablemente tendrán que moverse en una trayectoria no lineal. En el caso del mecanizado de trayectorias circulares de herramientas, la trayectoria de la línea central de la fresa de extremo es circular. Como era de esperar, esto se conoce como Interpolación circular.
Recorridos circulares de herramientas de corte
Todas las fresas de extremo giratorias tienen su propia velocidad angular en el diámetro exterior. Pero cuando la trayectoria de la herramienta es circular, se introduce un componente adicional, lo que resulta en una velocidad angular compuesta. Básicamente, esto significa que la velocidad del diámetro exterior viaja a una velocidad sustancialmente diferente a la esperada originalmente. La causa de la velocidad angular del compuesto se ve en la disparidad entre las longitudes de trayectoria de la herramienta.
Recorridos circulares internos de la herramienta
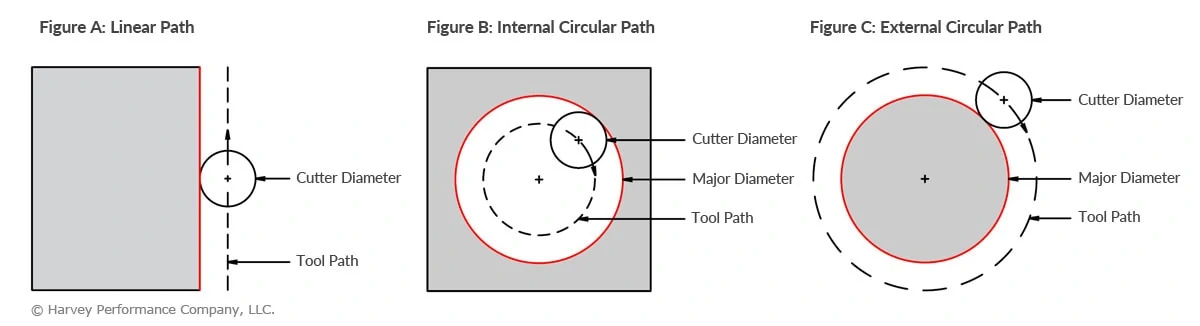
La figura A muestra la sección transversal de una herramienta de corte en un recorrido lineal, con los dientes con velocidad angular debido a la rotación de la herramienta, y el centro de la herramienta con alimentación lineal. Tenga en cuenta que la longitud de la trayectoria de la herramienta siempre será igual a la longitud del borde mecanizado. La Figura B muestra la misma herramienta de corte en un recorrido circular interno, como se hace al mecanizar un orificio. En este caso, la velocidad angular de los dientes se cambia como resultado de un componente adicional de la trayectoria circular del centro de la herramienta. El diámetro de la trayectoria de la herramienta es más pequeño que el del diámetro principal que se está cortando. O, en otras palabras, la longitud de la trayectoria de la herramienta es más corta que la longitud del borde mecanizado, lo que aumenta la velocidad angular de los dientes. Para evitar la sobrealimentación y la posibilidad de rotura de la herramienta, la velocidad angular aumentada de los dientes debe ser la misma que en el caso lineal de la Figura A. La fórmula siguiente se puede usar para reducir adecuadamente la velocidad de avance para el mecanizado interno:
Alimentación ajustada interna = (Diámetro mayor-Diámetro de la fresa) / (Diámetro mayor) × Alimentación lineal
Trayectorias de herramienta circulares externas
La figura C muestra la misma herramienta de corte en una trayectoria circular externa, como se hace al mecanizar un poste. En este caso, el diámetro de la trayectoria de la herramienta es mayor que el diámetro principal que se está cortando. Esto significa que la longitud de la trayectoria de la herramienta es más larga que la longitud del borde mecanizado, lo que resulta en una disminución de la velocidad angular. Para evitar el embotamiento prematuro y la vida útil deficiente de la herramienta debido al exceso de velocidad, utilice la fórmula siguiente para aumentar adecuadamente la velocidad de avance para el mecanizado externo. De esta manera, la velocidad angular disminuida de los dientes se hace igual que en el caso lineal de la Figura A.
Alimentación ajustada externa = (Diámetro principal + Diámetro de la fresa) / (Diámetro Principal) × Alimentación lineal
Optimice su rendimiento
Ajustando la alimentación de la manera proporcionada, las aplicaciones internas pueden evitar la rotura de la herramienta y el costoso tiempo de inactividad. Además, las aplicaciones externas pueden disfrutar de un rendimiento optimizado y tiempos de ciclo más cortos. También debe tenerse en cuenta que este enfoque se puede aplicar a piezas con esquinas radiadas, características elípticas y cuando se requiere interpolación helicoidal.