Los puntos de vida de los Engranajes

Los engranajes tienen un cierto número de puntos de vida (HP) dependiendo de su nivel. Los engranajes de nivel 1 tienen la menor cantidad de HP, mientras que los engranajes de nivel 12 tienen la mayor cantidad de HP.

La siguiente tabla muestra la cantidad de HP que tiene cada nivel de engranaje y qué mordazas pueden derrotar al engranaje en un solo golpe. Algunos gags pueden necesitar ser orgánicos.

Nivel	Puntos de vida	Mordazas de un solo golpe
1	6	Cupcake (6 daños) Maceta (10 daños) Vaso de agua (6 daños)
2	12	Cáscara de plátano (12 daños) Pistola de agua (12 daños) Saco de arena (18 daños)
3	20	Rastrillo (20 daños) Trompa de elefante (21 daños) Botella de Seltzer (21 daños)
4	30	Manguera contra incendios (30 daños) Yunque (30 daños) Canicas (35 daños)
5	42	Peso grande (45 daños) Tarta de Crema Entera Orgánica (44 daños) Arenas movedizas (50 daños)
6	56	Caja fuerte (60 daños) Trampilla (70 daños)
7	72	Trampilla orgánica (77 daños) Nube de tormenta (80 daños)
8	90	Cantante de ópera (90 daños) Pastel de cumpleaños (100 daños)
9	110	Pastel de Cumpleaños Orgánico (110 daños) Géiser orgánico (115 daños)
10	132	Pastel de Boda Orgánico (132 daños)
11	156	Piano de cola (170 daños) TNT (180 daños)
12	200	Ferrocarril orgánico (214 daños)

Fórmulas

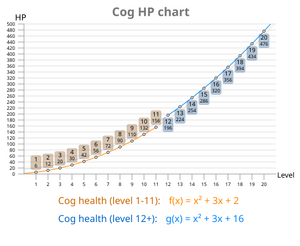
Un gráfico que muestra el crecimiento de la salud de los engranajes por su nivel. Se puede ver la diferencia de salud de los engranajes de nivel 12.

La fórmula para la salud de un engranaje puede ser:

$f (x) = x^{2}+3x + 2$

o de forma simplificada:

$f(x)=(x+1)\times (x+2)$

donde x es el nivel del engranaje y f (x) es una función que devuelve el valor de mantenimiento de los engranajes.

Por ejemplo, la fórmula funciona en el siguiente método para Engranajes de nivel cuatro, que tienen 30 HP:

$f(4)=(4+1)\tiempos (4+2)$ $f(4) = (5)\times (6)$ $f(4)=30$

La fórmula anterior se aplica a todos los niveles de engranaje, excepto el nivel 12, que tiene 200 HP.

Para recuperar el nivel del engranaje de un HP dado, en lugar de recuperar el HP del nivel, se puede usar la fórmula cuadrática donde n es el HP:

$x_{1,2}={\frac {-3\pm {\sqrt {9-4 * (2-n)}}}{2}}$

Por ejemplo, la ecuación se resolverá en el siguiente método para averiguar qué engranaje tendría 156 HP:

$x_{1,2}={\frac {-3\pm {\sqrt {9-4*(2-156)}}}{2}}$ $x_{1,2}={\frac {-3\pm {\sqrt {9-4*-154}}}{2}}$ $x_{1,2}={\frac {-3\pm {\sqrt {9+616}}}{2}}$ $x_{1,2}={\frac {-3\pm {\sqrt {625}}}{2}}$ $x_{1,2}={\frac {-3\pm 25}{2}}$ $x_{1}={\frac {-3-25}{2}},x_{2}={\frac {-3+25}{2}}$ $x_{1}={\frac {-28}{2}},x_{2}={\frac {22}{2}}$ $x_{1}=-14,x_{2}=11$

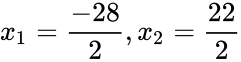
Puesto que f(x) es una función de una parábola y ninguna de las soluciones es el valor mínimo de la función, hay dos respuestas para la ecuación: -14, que no es un nivel de engranaje real; y 11, que es un nivel real.

Aunque esta fórmula funciona para todos los niveles de engranaje, al ir más allá de los niveles de engranaje regulares, esta fórmula comienza a ser inaplicable en la práctica debido a los números complejos. Para cualquier valor de n inferior a -0,25, esta ecuación introduce números complejos, que todavía funcionan en teoría, pero no en la práctica.

Trivia

Aunque los engranajes de nivel 12 deben tener 182 HP, en su lugar tienen 200, lo que es esencialmente un aumento del 10%. De acuerdo con la fórmula, un engranaje con 200 HP debe ser de aproximadamente nivel 12.65 (o aproximadamente -15.65, aunque los valores negativos no son compatibles con los niveles de engranaje).
Según la fórmula, el Director de Marketing de Emboscadas tendría 2.652 HP, dado que es de nivel 50.

Fórmulas

Trivia

Published by admin

Deja una respuesta Cancelar la respuesta