Tiempo de Sincronización en Sistemas Distribuidos

Si está familiarizado con sitios web como facebook.com o Google.com, tal vez no menos de una vez se ha preguntado cómo estos sitios web pueden manejar millones o incluso decenas de millones de solicitudes por segundo. ¿Habrá algún servidor comercial único que pueda soportar esta gran cantidad de solicitudes, de manera que cada solicitud se pueda servir a tiempo para los usuarios finales?

Profundizando en este tema, llegamos al concepto de sistemas distribuidos, una colección de computadoras (o nodos) independientes que se presentan a sus usuarios como un único sistema coherente. Esta noción de coherencia para los usuarios es clara, ya que creen que están tratando con una sola máquina gigantesca que toma la forma de múltiples procesos que se ejecutan en paralelo para manejar lotes de solicitudes a la vez. Sin embargo, para las personas que entienden la infraestructura del sistema, las cosas no resultan tan fáciles como tales.

Para miles de máquinas independientes que se ejecutan simultáneamente y que pueden abarcar varias zonas horarias y continentes, se deben proporcionar algunos tipos de sincronización o coordinación para que estas máquinas colaboren de manera eficiente entre sí (para que puedan aparecer como una sola). En este blog, discutiremos la sincronización del tiempo y cómo logra consistencia entre las máquinas en el orden y la causalidad de los eventos.

El contenido de este blog se organizará de la siguiente manera:

1. Sincronización de reloj
2. Relojes lógicos
3. Para llevar
4. ¿Qué sigue?

Relojes físicos

En un sistema centralizado, el tiempo es inequívoco. Casi todas las computadoras tienen un “reloj en tiempo real” para realizar un seguimiento del tiempo, generalmente sincronizado con un cristal de cuarzo mecanizado con precisión. Basado en la oscilación de frecuencia bien definida de este cuarzo, el sistema operativo de una computadora puede monitorear con precisión el tiempo interno. Incluso cuando la computadora se apaga o se apaga, el cuarzo sigue funcionando gracias a la batería CMOS, una pequeña central eléctrica integrada en la placa base. Cuando la computadora se conecta a la red (Internet), el sistema operativo se pone en contacto con un servidor de temporizador, que está equipado con un receptor UTC o un reloj preciso, para restablecer con precisión el temporizador local utilizando el Protocolo de tiempo de red, también llamado NTP.

Aunque esta frecuencia del cuarzo cristalino es razonablemente estable, es imposible garantizar que todos los cristales de diferentes computadoras operen exactamente a la misma frecuencia. Imagine un sistema con n computadoras, cuyos cristales funcionan a velocidades ligeramente diferentes, lo que hace que los relojes se desincronicen gradualmente y den valores diferentes cuando se leen. La diferencia en los valores de tiempo causada por esto se denomina sesgo de reloj.

Bajo esta circunstancia, las cosas se complicaron por tener varias máquinas separadas espacialmente. Si el uso de múltiples relojes físicos internos es deseable, ¿cómo los sincronizamos con relojes del mundo real? ¿Cómo los sincronizamos entre sí?

Protocolo de tiempo de red

Un enfoque común para la sincronización de pares entre computadoras es a través del uso del modelo cliente-servidor, es decir, permitir que los clientes contacten con un servidor de tiempo. Vamos a considerar el siguiente ejemplo con 2 máquinas a y B:

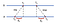
Primero, A envía una solicitud con marca de tiempo con el valor t to a B. B, a medida que llega el mensaje, registra la hora de recepción t from de su propio reloj local y las respuestas con un mensaje marcado con T₂, cargando el valor registrado previamente t.. Por último, A, al recibir la respuesta de B, registra la hora de llegada t T. Para tener en cuenta el retraso en la entrega de mensajes, calculamos δ = = t T-t., Δ₂ = t.-T₂. Ahora, se estima que el desplazamiento de Un familiar a B es:

Basado en θ, podemos ralentizar el reloj de A o ajustarlo para que las dos máquinas puedan sincronizarse entre sí.

Dado que NTP es aplicable en pares, el reloj de B también se puede ajustar al de A. Sin embargo, no es prudente ajustar el reloj en B si se sabe que es más preciso. Para resolver este problema, NTP divide los servidores en estratos, es decir, servidores de clasificación, para que los relojes de los servidores menos precisos con rangos más pequeños se sincronicen con los de los más precisos con rangos más altos.

Berkeley Algorithm

En contraste con los clientes que contactan periódicamente con un servidor de tiempo para una sincronización de tiempo precisa, Gusella y Zatti, en 1989 Berkeley Unix Paper , propusieron el modelo cliente-servidor en el que el servidor de tiempo (demonio) sondea cada máquina periódicamente para preguntar qué hora es allí. Basado en las respuestas, calcula el tiempo de ida y vuelta de los mensajes, promedia el tiempo actual con ignorancia de cualquier valor atípico en los valores de tiempo, y “le dice a todas las demás máquinas que adelanten sus relojes a la nueva hora o que ralenticen sus relojes hasta que se logre alguna reducción especificada” .

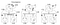
Relojes lógicos

Demos un paso atrás y reconsideremos nuestra base de marcas de tiempo sincronizadas. En la sección anterior, asignamos valores concretos a los relojes de todas las máquinas participantes, a partir de ahora pueden acordar una línea de tiempo global en la que ocurren los eventos durante la ejecución del sistema. Sin embargo, lo que realmente importa a lo largo de la línea de tiempo es el orden en que ocurren los eventos relacionados. Por ejemplo, si de alguna manera sólo necesitamos saber de Un evento que sucede antes de que el evento B, no importa si Tₐ = 2, Tᵦ = 6 o Tₐ = 4, Tᵦ = 10, mientras Tₐ < Tᵦ. Esto cambia nuestra atención al reino de los relojes lógicos, donde la sincronización está influenciada por la definición de Leslie Lamport de la relación “sucede antes”.

Los relojes lógicos de Lamport

En su fenomenal 1978 paper Time, Clocks, and the Ordering of Events in a Distributed System , Lamport definió la relación “sucede antes” → ” de la siguiente manera:

1. Si a y b son eventos en el mismo proceso, y a viene antes de b, entonces a→b.

2. Si a es el envío de un mensaje por un proceso y b es la recepción del mismo mensaje por otro proceso, entonces a→b.

3. Si a→b y b→c, entonces a→c.

Si los eventos x, y ocurren en diferentes procesos que no intercambian mensajes, ni x → y ni y → x son verdaderos, se dice que x e y son simultáneos. Dada una función C que asigna un valor de tiempo C(a) para un evento en el que todos los procesos están de acuerdo, si a y b son eventos dentro del mismo proceso y a ocurre antes de b, C(a) < C (b)*. De manera similar, si a es el envío de un mensaje por un proceso y b es la recepción de ese mensaje por otro proceso, C(a) < C(b) **.

Ahora veamos el algoritmo que Lamport propuso para asignar tiempos a eventos. Considere el siguiente ejemplo con un grupo de 3 procesos A, B, C:

Los relojes de estos 3 procesos funcionan en su propio tiempo y están inicialmente fuera de sincronización. Cada reloj se puede implementar con un contador de software simple, incrementado en un valor específico cada T unidades de tiempo. Sin embargo, el valor por el que se incrementa un reloj difiere según el proceso: 1 para A, 5 para B y 2 para C.

En el momento 1, A envía el mensaje m1 a B. En el momento de la llegada, el reloj en B lee 10 en su reloj interno. Dado que el mensaje enviado estaba marcado con la hora 1, el valor 10 en el proceso B es ciertamente posible (podemos inferir que se necesitaron 9 ticks para llegar a B desde A).

Ahora considere el mensaje m2. Sale de B a 15 y llega a C a 8. Este valor de reloj en C es claramente imposible ya que el tiempo no puede retroceder. Desde ** y el hecho de que m2 salga a las 15, debe llegar a las 16 o más tarde. Por lo tanto, tenemos que actualizar el valor de tiempo actual en C para que sea mayor que 15 (agregamos +1 al tiempo para simplificar). En otras palabras, cuando llega un mensaje y el reloj del receptor muestra un valor que precede a la marca de tiempo que señala la salida del mensaje, el receptor adelanta su reloj para que sea una unidad de tiempo más que la hora de salida. En la figura 6, vemos que m2 ahora corrige el valor del reloj en C a 16. Del mismo modo, m3 y m4 llegan a 30 y 36 respectivamente.

Del ejemplo anterior, Maarten van Steen et al formula el algoritmo de Lamport de la siguiente manera:

1. Antes de ejecutar un evento (es decir, enviar un mensaje a través de la red, …), p incre incrementa c C: c

2. Cuando el proceso p sends envía el mensaje m al proceso Pj, establece la marca de tiempo ts(m) de m igual a c after después de haber ejecutado el paso anterior.

3. Al recibir un mensaje m, el proceso Pj ajusta su propio contador local como Cj < – max{Cj, ts (m)}, después de lo cual ejecuta el primer paso y entrega el mensaje a la aplicación.

Relojes Vectoriales

Recuerde volver a la definición de Lamport de la relación “sucede antes”, si hay dos eventos a y b tales que a ocurre antes de b, entonces a también se coloca en ese orden antes de b, es decir, C(a) < C(b). Sin embargo, esto no implica causalidad inversa, ya que no podemos deducir que a vaya antes que b simplemente comparando los valores de C(a) y C(b) (la prueba se deja como un ejercicio al lector).

Para obtener más información sobre el orden de eventos en función de su marca de tiempo, se propone Vectoriales Clocks, una versión más avanzada del Reloj Lógico de Lamport. Para cada proceso p of del sistema, el algoritmo mantiene un vector vc with con los siguientes atributos:

1. vcᵢ: reloj lógico local en p P, o el número de eventos que han ocurrido antes de la marca de tiempo actual.

2. Si vc = = k, p knows sabe que k eventos han ocurrido en Pj.

El algoritmo de los relojes Vectoriales es el siguiente:

1. Antes de ejecutar un evento, p records registra que un nuevo evento ocurre en sí mismo ejecutando vc

2. Cuando p sends envía un mensaje m a Pj, establece la marca de tiempo ts (m) igual a vc after después de haber ejecutado el paso anterior.

3. Cuando se recibe el mensaje m, el proceso Pj actualiza cada k de su propio reloj vectorial: VCJ ← max { VCj, ts (m)}. Luego continúa ejecutando el primer paso y entrega el mensaje a la aplicación.

Por estos pasos, cuando un proceso Pj recibe un mensaje m del proceso p with con marca de tiempo ts (m), conoce el número de eventos que han ocurrido en p cas precedido casualmente al envío de m. Además, Pj también conoce los eventos que han sido conocidos por p. sobre otros procesos antes de enviar m. (Sí, es cierto, si está relacionando este algoritmo con el Protocolo de Chismes🙂).

Con suerte, la explicación no te deja rascándote la cabeza por mucho tiempo. Vamos a sumergirnos en un ejemplo para dominar el concepto:

En este ejemplo, tenemos tres procesos p alternatively, P₂ y p P intercambiando mensajes alternativamente para sincronizar sus relojes. p sends envía el mensaje m1 en el tiempo lógico vc = = (1, 0, 0) (paso 1) a P₂. P₂, al recibir m1 con marca de tiempo ts (m1) = (1, 0, 0), ajusta su tiempo lógico VC₂ a (1, 1, 0) (paso 3) y envía el mensaje m2 de vuelta a p with con marca de tiempo (1, 2, 0) (paso 1). De manera similar, el proceso p accepts acepta el mensaje m2 de P₂, altera su reloj lógico a (2, 2, 0) (paso 3), después de lo cual envía el mensaje m3 a p at en (3, 2, 0). p adjusts ajusta su reloj a (3, 2, 1) (paso 1) después de recibir el mensaje m3 de p.. Más tarde, toma el mensaje m4, enviado por P₂ en (1, 4, 0), y por lo tanto ajusta su reloj a (3, 4, 2) (paso 3).

En función de cómo adelantamos los relojes internos para la sincronización, el evento a precede al evento b si para todos los k, ts(a) ≤ ts(b), y hay al menos un índice k’ para el cual ts(a) < ts(b). No es difícil ver que (2, 2, 0) precede a (3, 2, 1), (1, 4, 0) y (3, 2, 0) pueden entrar en conflicto unos con otros. Por lo tanto, con los relojes vectoriales, podemos detectar si hay o no una dependencia causal entre dos eventos cualesquiera.

Para llevar

Cuando se trata del concepto de tiempo en el sistema distribuido, el objetivo principal es lograr el orden correcto de los eventos. Los eventos se pueden posicionar en orden cronológico con Relojes Físicos o en orden lógico con los Relojes Lógicos y los Relojes Vectoriales de Lamtport a lo largo de la línea de tiempo de ejecución.

¿Qué sigue?

A continuación, repasaremos cómo la sincronización de tiempo puede proporcionar respuestas sorprendentemente simples a algunos problemas clásicos en sistemas distribuidos: mensajes a lo sumo de uno , consistencia de caché y exclusión mutua .

Leslie Lamport: Hora, Relojes y Orden de Eventos en un Sistema Distribuido. 1978.

Barbara Liskov: Usos prácticos de relojes sincronizados en sistemas distribuidos. 1993.

Maarten van Steen, Andrew S. Tanenbaum: Sistemas distribuidos. 2017.

Barbara Liskov, Liuba Shrira, John Wroclawski: Mensajes Eficientes A Lo Sumo Una Vez Basados en Relojes Sincronizados. 1991.

Cary G. Gray, David R. Cheriton: Arrendamientos: Un Mecanismo Eficiente Tolerante a Fallos para la Consistencia de la Caché de Archivos Distribuida. 1989.

Ricardo Gusella, Stefano Zatti: La Precisión de la Sincronización de Reloj Alcanzada por el TEMPO en Berkeley UNIX 4.3 BSD. 1989.