5.8 Tiesitkö, että suurin osa sademääristä tulee törmäys-koalitiosta?
5.8 Tiesitkö, että suurin osa sademääristä tulee törmäys-koalitiosta?
sadepisaroiksi kasvamisprosesseja on kahdenlaisia: lämpimän pilven prosesseja ja kylmän pilven prosesseja. Lämpimissä pilvissä prosesseihin liittyy vain nestepisaroita. Kylmissä pilvissä prosesseissa voi olla mukana vain kiinteitä hiukkasia sekä sekafaaseja (sekä ylijäähtynyttä nestettä että jäätä). Jotkin tärkeimmistä prosesseista liittyvät pisaroiden törmäyksiin, olivatpa ne nestemäisiä tai kiinteitä.
törmäyksiä
törmäyksiä tapahtuu sekä kylmissä että lämpimissä pilvissä ja niihin voi liittyä joko nestepisaroita tai kiinteitä hiukkasia tai molempia.
- Collision-Coalescence: Large liquid drop scavenges smaller liquid drops as it falls.
- Riming: putoava jää kerää itseensä nestemäistä vettä, joka jäätyy pinnaltaan.
- kaapata nukleaatio: Suuri nestepisara kaappaa pienen jäähiukkasen, joka toimii jään ytimenä ja saa suuren pisaran jäätymään. Kerättävä hiukkanen voi olla joko jääydin (IN) tai jääkappale, joka on myös hyvä jääydin. Kummassakin tapauksessa alijäähtynyt nestepisara jäätyy joutuessaan kosketuksiin IN: n kanssa.
- Aggregation: Falling snowflake scavenges other snowflakes that aggregate to make a larger snowflake bundle.
levossa olevassa pilvipisarassa painovoima on ainoa ulkoinen voima. Kun pilvipisara alkaa pudota, ilmanvastus muodostaa toisen voiman, jota kutsutaan vedoksi, joka on nopeuden funktio.
alle sekunnissa hiukkanen saavuttaa putoamisnopeuden siten, että vastusvoima tasapainottaa painovoiman täsmälleen ja nopeudesta tulee vakio. Tätä nopeutta kutsutaan terminaalinopeudeksi. Koska painovoima riippuu pisaran tilavuudesta, se menee pudotussäteen kuutiona. Sen sijaan veto vaikuttaa pisaran pintaan, joten se riippuu pudotusalueesta ja menee pudotussäteen neliönä (kertaa nopeus). Kun painovoima-ja vetovoimat asetetaan yhtä suuriksi kuin muut ja sitten ratkaistaan terminaalin nopeus, on helppo osoittaa, että terminaalin nopeuden tulisi vaihdella lineaarisesti pudotussäteen kanssa. Mittaukset tukevat tätä lineaarista suhdetta. Esimerkiksi 50 µm: n säteispudotuksen terminaalinopeus on noin 0,3 m s–1, kun taas 10 kertaa suuremman (500 µm: n säde) pisaran terminaalinopeus on noin 4 m s–1, mikä vain hieman enemmän kuin-10: N kerroin.
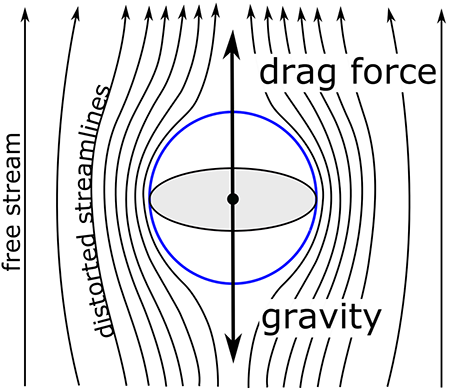
pilvipisaran kasvu sadepisaraksi törmäyksen voimasta-koalitio saadaan yhtälöstä:
d m L dt =alue pyyhkäistiin ulos⋅keräystehokkuus⋅nopeusero⋅nestemäisen veden pitoisuus d m L dt = A G ⋅ E C ⋅( v L − v s) π LWC d m L dt =π ( r l + r s ) 2⋅e c ⋅ (v L − v s) ⋅ LWC tämä yhtälö ei toimi oikein yhteensopimattoman selaimen takia. Katso teknisten vaatimusten suunta luettelo yhteensopivista selaimista.
- mL on putoavan suuren pisaran massa,
- AG on geometrinen poikkipinta-ala, jolle putoavan suuren pisaran ja alla olevien monien pisaroiden väliset törmäykset ovat mahdollisia,
- Ec on törmäyshalenssitehokkuus (ts., keräystehokkuus), joka on se murto-osa todellisesta poikkipinta-alasta, joka pyyhkäistään pois verrattuna geometrisesti mahdolliseen poikkipinta-alaan (pienemmät pisarat voivat seurata ilmavirtauksia ja kiertää ison pudotuksen) (katso kuva alla),
- VL on suuren pudotuksen nopeus ja vs on alla olevien pienempien, hitaampien putoavien pisaroiden nopeus,
- ja LWC on nestemäisen veden pitoisuus.
alla oleva kuva antaa hyvän käsitteellisen kuvan törmäys–koalitiosta. Keräinpisaran täytyy pudota nopeammin kuin pienemmän kerätyn pisaran, jotta ne voivat törmätä toisiinsa. Kun ilmavirtaukset kumartuvat pisaran ympäri, ne kuljettavat pienempiä pisaroita mukanaan pisaran ympäri, ja tehollinen poikkipinta-ala jää pienemmäksi kuin varsinainen poikkipinta-ala, joka on yksinkertaisesti sellaisen levyn poikkipinta-ala, jonka säde on suuren keräinpisaran ja pienempien kerättyjen pisaroiden säteiden summa. Pudotusten kasvaessa niillä on liikaa inertiaa seurata ilmavirtauksia, jolloin törmäys on todennäköisempää.
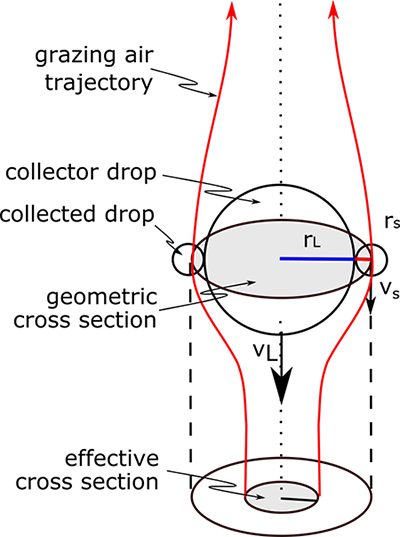
Ec on pieni 10 µm: n pisaroille, joten satunnaisessa prosessissa jotkut pisarat kasvavat suuremmiksi kuin toiset ja alkavat kerätä pienempiä pisaroita (katso kuva alla). EY kasvaa, kun putoavan pisaran säde kasvaa. Kun suurempi putoava pisara saa säteensä yli 100 µm, sen törmäyshalesenssitehokkuus on erittäin hyvä kaikille pienemmille pudotuksille noin 10-20 µm: n kokoihin.
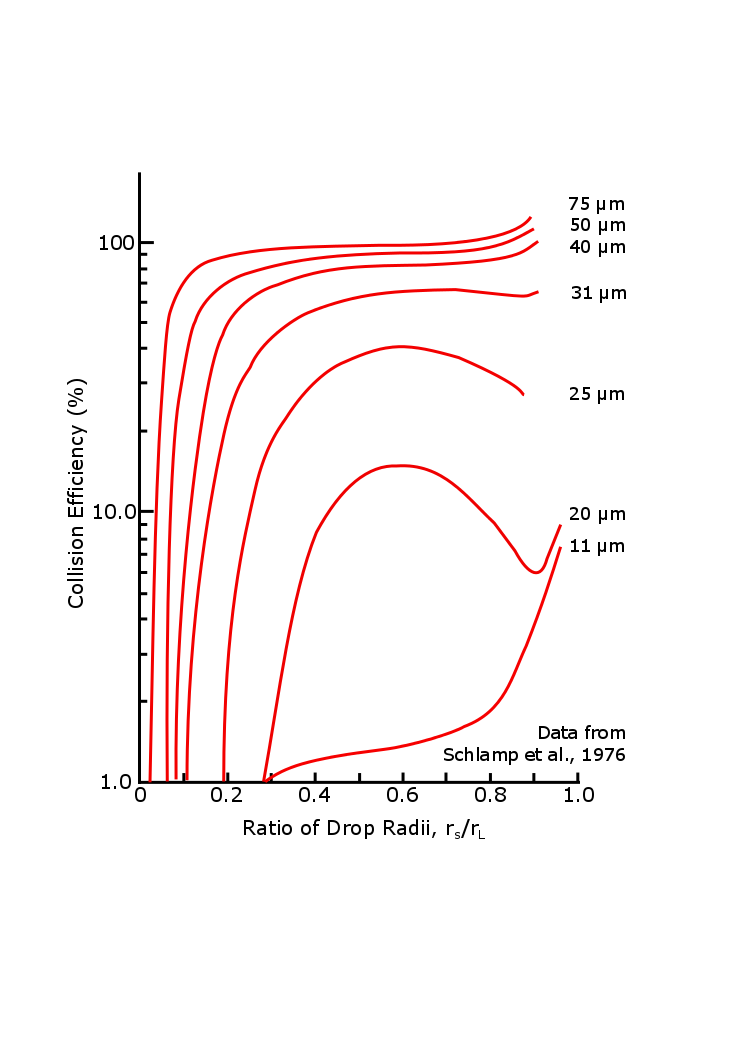
kun keräävä pisara on saavuttanut muutaman sadan µm: n säteen, se putoaa nopeasti (vL >> vs) ja sen törmäyshalenssitehokkuus on lähes 100%. Kirjoita yhtälö 5.16 uudelleen seuraavasti: (1) Ec yhtä suuri kuin 1, (2) vL >> vs, (3) vL = vakio x rL, (4) mL = 4plnrL3/3 , ja (5) ratkaise DRL/dt. Kun otat nämä vaiheet, voit osoittaa, että drL / dt on verrannollinen rL: ään. Toisin sanoen, mitä suurempi pudotus on, sitä nopeammin se kasvaa. Muuttujien (rL ja t) erottaminen ja integrointi RL = 0: sta T = 0: sta RL: n ja t: n mielivaltaisiin arvoihin paljastaa, että rL kasvaa eksponentiaalisesti ajan myötä:
r D ∝exp (aika) tämä yhtälö ei renderöi oikein yhteensopimattoman selaimen takia. Katso teknisten vaatimusten suunta luettelo yhteensopivista selaimista.
päätenopeuden ja pudotussäteen suhteellisuusvakion ollessa 0.8 x 10-3 s–1 ja LWC = 1 g m–3, voidaan osoittaa, että pisara voi kasvaa 50 µm: sta 1000 µm: iin törmäyshalenssilla vain 25 minuutissa. Aktivoidut pilvipisarat kasvavat siis 10-20 µm: iin höyrykertymän hitaalla kasvulla (ajan neliöjuuri). Kun törmäys-koalitio alkaa ja tuottaa muutaman ison pisaran, ne voivat kasvaa eksponentiaalisesti ajan kanssa.
pienemmät pisarat ovat tyypillisesti pallomaisia. Kun nämä pisarat saavat olla yli millimetrin säteellä, ne vääristyvät yhä enemmän, jolloin pohja on litistynyt vetovoimien vuoksi, ja ne näyttävät hieman hampurilaissämpylän yläpuolelta. Niitä voidaan edelleen vääristellä niin, että pullamaisen muodon keskiosa saa vetovoimat nostettua ylöspäin niin, että pudotus saa ylösalaisin olevaa kulhoa muistuttavan muodon.
lopulta pisarat hajoavat, joko ohentumalla keskeltä niin, että ne hajoavat palasiksi, tai törmäämällä muihin pisaroihin niin kovaa, että filamentit tai nestelevyt katkeavat muodostaen muita pisaroita. Nämä prosessit luovat koko valikoiman tippoja. Näin sade koostuu pisaroista, joilla on laaja kirjo kokoa. Seuraava video (2:50) “How Raindrops are Formed” alkaa pelkistetyllä näkymällä ilmakehän veden kiertokulusta, mutta näyttää sitten esimerkkejä putoavasta pisarasta, törmäyksestä ja pilven hajoamisesta.
nyt tämä on tuttu näky. Auringon lämpö saa kasvien, järvien ja valtamerten veden muuttumaan nesteestä höyryksi. Korkealla ilmakehässä vesihöyry sitten jäähtyy ja tiivistyy kaasusta takaisin nesteeksi. Tällöin nestemäinen vesi putoaa takaisin pintaan sateen, lumen, jään tai rakeiden muodossa. Vesi valuu puroihin järviin ja valtameriin tai varastoituu maahan tai lumipolulle. Tämä on veden kiertokulku ja se kuvaa kaikkein tärkeintä resurssiamme, joka liikkuu koko maapallon järjestelmässä, mutta kuten useimmat asiat maailmassamme, kun katsomme pieniä osia, jotka muodostavat kokonaisuuden, voimme oppia paljon lisää ilmiöstä. Ota yhden sadepisaran muoto. Ilmakehän pienet vesipisarat ovat muodoltaan pallomaisia vesimolekyylien pintajännityksen tai ihon vuoksi. Kun nämä pisarat kasvavat, niistä tulee painavampia ja ne alkavat pudota ilmassa. Pudotessaan sadepisara törmää muihin pisaroihin ja kasvaa edelleen. Nämä suuremmat sadepisarat putoavat ilman läpi nopeammin ilmanvastus pisaran alapuolelta saa pisaran pohjan litistymään, jolloin pisara näyttää hampurilaissämpylältä. Kun pisara jatkaa putoamistaan ja kasvaa jossain vaiheessa, siitä tulee liian suuri pintajännitys pitämään sitä koossa, joten sadepisara hajoaa pienemmiksi spiraakkelipisaroiksi. Niiden prosessien tutkiminen, joita emme näe paljain silmin, ei ole mitään uutta. Tiede ja teknologia vievät toisiaan eteenpäin ja johtavat usein oivalluksiin ja löytöihin matkan varrella. Kun keksintö nopea valokuvaus näimme lopulta kaikkein peruselementit vetisen planeettamme toiminnassa. Sen ymmärtäminen, miten pieni sadepisara putoaa ilmakehän läpi, tekee muutakin kuin kumoaa sen myytin, että sadepisara putoaa kuin kyynelpisara. Sillä on itse asiassa merkitystä erityisesti pohjatutkien sademäärien mittaamisessa. Maatutkat tarkastelevat sadepisaroiden sivuja ja arvioivat sitten pysty-ja vaakasuorat huokaukset. Raskaamman ja tasaisemman pisaran avulla tutkat voivat tunnistaa raskaammat sademäärät. Itse asiassa GPM-satelliitin kaksi tutkaa voivat myös mitata pisarakokoja avaruudesta, joten sadepisaroiden tarkempi tarkastelu antaa meille tarkemman kuvan siitä, miten maailmanlaajuinen sademäärä on muotoutumassa.
Riming, capture nukleation, ja aggregointi, on olemassa samanlaisia yhtälöitä termit samanlaisia kuin yhtälö 5.16—alue pyyhkäisi pois, keräystehokkuus, suhteellinen nopeus, ja nesteen tai kiinteän massan pitoisuus pienempiä pisaroita tai jäätä. Nämä ovat tyypillisesti hieman monimutkaisempia, jos jää ei ole pallomainen, mutta käsitteet ovat samat. Nämä jään törmäys-koalitio prosessit pystyvät tuottamaan tarpeeksi suuria jäähiukkasia, ja jos nämä hiukkaset lämpenevät kulkiessaan pilven lämpimän osan läpi, ne voivat muuttua nestemäiseksi sateeksi. Merkittävä osa kesän sateista voi tulla Jäätymisrajan yläpuolisista jäätymisistä pilvissä.