aikasynkronointi hajautetuissa järjestelmissä

jos huomaat tuntevasi esimerkiksi verkkosivut facebook.com tai googlettaa.com, ehkä vähintään kerran olet ihmetellyt, miten nämä sivustot voivat käsitellä miljoonia tai jopa kymmeniä miljoonia pyyntöjä sekunnissa. Onko olemassa mitään yhtä kaupallista palvelinta, joka kestää tämän valtavan määrän pyyntöjä sillä tavalla, että jokainen pyyntö voidaan toimittaa ajoissa loppukäyttäjille?

Sukeltaessamme syvemmälle tähän asiaan päädymme käsitteeseen hajautetut järjestelmät, kokoelma itsenäisiä tietokoneita (tai solmuja), jotka näyttäytyvät käyttäjilleen yhtenäisenä yhtenäisenä järjestelmänä. Tämä johdonmukaisuuden käsite käyttäjille on selvä, koska he uskovat käsittelevänsä yhtä ihmismäistä konetta, joka muodostuu useista rinnakkain käynnissä olevista prosesseista pyyntöjen käsittelemiseksi kerralla. Järjestelmäinfrastruktuuria ymmärtäville ihmisille asiat eivät kuitenkaan ole niin helppoja.

tuhansille samanaikaisesti toimiville itsenäisille koneille, jotka voivat ulottua usealle aikavyöhykkeelle ja mantereelle, on annettava tietyntyyppinen synkronointi-tai koordinointijärjestelmä, jotta nämä koneet voivat tehdä tehokasta yhteistyötä keskenään (jotta ne voivat esiintyä yhtenä koneena). Tässä blogissa keskustelemme ajan synkronoinnista ja siitä, miten se saavuttaa johdonmukaisuuden koneiden välillä tilaamisesta ja tapahtumien syy-seuraussuhteesta.

tämän blogin sisältö on järjestetty seuraavasti:

1. kellojen synkronointi
2. loogiset kellot
3. ota pois
4. mitä seuraavaksi?

fyysiset kellot

keskitetyssä järjestelmässä aika on yksiselitteinen. Lähes kaikissa tietokoneissa on ajan seuraamiseen tarkoitettu” reaaliaikainen kello”, joka on yleensä synkronoitu tarkasti työstetyn kvartsikiteen kanssa. Tämän kvartsin hyvin määritellyn taajuuden värähtelyn perusteella tietokoneen käyttöjärjestelmä pystyy tarkasti seuraamaan sisäistä aikaa. Vaikka tietokone sammutetaan tai se sammuu, kvartsi tikittää edelleen CMOS-akun ansiosta, joka on emolevyyn integroitu pieni voimanpesä. Kun tietokone muodostaa yhteyden verkkoon (Internet), käyttöjärjestelmä ottaa yhteyttä ajastinpalvelimeen, joka on varustettu UTC-vastaanottimella tai tarkalla kellolla, jotta paikallinen ajastin voidaan palauttaa tarkasti verkon Aikaprotokollalla, jota kutsutaan myös NTP: ksi.

vaikka tämä kidekvartsin taajuus on kohtuullisen vakaa, on mahdotonta taata, että kaikki eri tietokoneiden kiteet toimivat täsmälleen samalla taajuudella. Kuvitelkaa järjestelmä, jossa on n-tietokoneet, joiden jokainen kide kulkee hieman eri nopeudella, mikä saa kellot vähitellen poikkeamaan synkronoinnista ja antamaan eri arvoja, kun ne luetaan. Tästä aiheutuvaa aika-arvojen eroa kutsutaan kellon vinoksi.

tässä tilanteessa asiat menivät sotkuiseksi, kun oli useita tilallisesti erotettuja koneita. Jos useiden sisäisten fyysisten kellojen käyttö on suotavaa, miten synkronoimme ne reaalimaailman kellojen kanssa? Miten synkronoimme ne keskenään?

Verkkoaikaprotokolla

yhteinen lähestymistapa tietokoneiden väliseen parisynkronointiin on client-server-mallin käyttö eli anna asiakkaiden ottaa yhteyttä aikapalvelimeen. Tarkastellaan seuraavaa esimerkkiä 2 koneet A ja B:

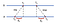
ensin a lähettää B: lle aikaleimatun pyynnön, jonka arvo on T. B kirjaa viestin saapuessa T₁: n vastaanottoajan omasta paikallisesta kellostaan ja vastaa viestiin T₂-merkinnällä varustetulla viestillä, jossa on aiemmin kirjattu arvo t₂. Lopuksi A, saatuaan vastauksen B, kirjaa saapumisajan T₃. Viestien lähettämisen viivästymisen huomioon ottamiseksi laskemme Δ₁ = T₁-T₀, δ₂₂ = T₂-T₂. Nyt arvioitu siirtymä suhteessa B on:

θ: n perusteella voidaan joko hidastaa A: n kelloa tai kiinnittää se niin, että kaksi konetta voidaan synkronoida keskenään.

koska NTP on pareittain sovellettavissa, B: n kello voidaan säätää myös A: n kellon tasolle. On kuitenkin epäviisasta säätää kelloa B: ssä, jos sen tiedetään olevan tarkempi. Ongelman ratkaisemiseksi NTP jakaa palvelimet kerrostumiin eli paremmuusjärjestykseen siten, että vähemmän tarkkojen palvelimien kellot, joilla on pienempi arvo, synkronoidaan tarkempien palvelimien kelloihin, joilla on korkeampi arvo.

Berkeleyn algoritmi

Gusella ja Zatti ehdottivat vuonna 1989 Berkeley Unix paper-lehdessä asiakas-palvelinmallia, jossa aikapalvelin (daemon) tarkkailee jokaista konetta määräajoin kysyäkseen, mihin aikaan se on siellä. Vastausten perusteella se laskee viestien edestakaisen matkan ajan, laskee nykyisen ajan ilman, että aika-arvoissa on poikkeamia, ja “käskee kaikkia muita koneita siirtämään kellojaan uuteen aikaan tai hidastamaan kellojaan, kunnes jokin tietty vähennys haw on saavutettu” .

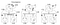
loogiset kellot

otetaan askel taaksepäin ja mietitään uudelleen synkronoitujen aikaleimojen pohjaamme. Edellisessä osassa, annamme konkreettisia arvoja kaikkien osallistuvien koneiden kellot, vastedes he voivat sopia globaalin aikajanan, jossa tapahtumat tapahtuvat suorittamisen aikana järjestelmän. Koko aikajanalla on kuitenkin merkitystä sillä, missä järjestyksessä siihen liittyvät tapahtumat tapahtuvat. Esimerkiksi, jos jotenkin meidän täytyy vain tietää, tapahtuma A tapahtuu ennen tapahtumaa B, se ei ole väliä, jos Tₐ = 2, Tᵦ = 6 tai Tₐ = 4, Tᵦ = 10, niin kauan kuin Tₐ < Tᵦ. Tämä siirtää huomiomme loogisten kellojen valtakuntaan, jossa synkronointiin vaikuttaa Leslie Lamportin määritelmä “tapahtuu-ennen” – suhteesta .

Lamportin loogiset kellot

ilmiömäisessä vuoden 1978 paperissaan Time, Clocks, and the order of Events in a Distributed System Lamport määritteli “happens-before” – suhteen ” → ” seuraavasti:

1. Jos a ja b ovat saman prosessin tapahtumia ja a tulee ennen b: tä, niin A→B.

2. Jos A on viestin lähettäminen yhdellä prosessilla ja b saman viestin vastaanottaminen toisella prosessilla, niin A→B.

3. Jos A→B ja b→c, niin A→c.

jos tapahtumat x, y esiintyvät eri prosesseissa, jotka eivät vaihda viestejä, ei x → y eikä y → x ole tosi, X: n ja y: n sanotaan olevan samanaikaisia. Koska C-funktio määrittää aika-arvon C (a) tapahtumalle, josta kaikki prosessit ovat samaa mieltä, Jos A ja b ovat saman prosessin tapahtumia ja a tapahtuu ennen b: tä, C(a) < C(b)*. Vastaavasti jos A on viestin lähettäminen yhdellä prosessilla ja b viestin vastaanottaminen toisella prosessilla, C (a) < C (b)**.

Tarkastellaanpa nyt algoritmia, jota Lamport ehdotti aikojen osoittamiseksi tapahtumille. Tarkastellaan seuraavaa esimerkkiä klusterin 3 prosesseja A, B, C:

näiden kolmen prosessin kellot toimivat omalla ajoituksellaan ja ovat aluksi epätahdissa. Jokainen kello voidaan toteuttaa yksinkertaisella ohjelmistolaskurilla, jota korotetaan tietyllä arvolla joka T-aikayksiköllä. Arvo, jolla kelloa korotetaan, vaihtelee kuitenkin prosessikohtaisesti: 1 A: lle, 5 B: lle ja 2 C: lle.

ajanhetkellä 1 A lähettää viestin m1 B: lle. saapumishetkellä B: n kello lukee sisäisessä kellossaan 10. Koska viesti on lähetetty oli aikaleimattu aika 1, arvo 10 prosessissa B on varmasti mahdollista (voimme päätellä, että kesti 9 punkit saapua B alkaen A).

nyt tarkastellaan viestiä m2. Se lähtee B: stä kello 15 ja saapuu C: hen kello 8. Kellon arvo C: ssä on selvästi mahdoton, koska aika ei voi mennä taaksepäin. Alkaen ** ja se, että m2 lähtee klo 15, sen täytyy saapua klo 16 tai myöhemmin. Siksi meidän on päivitettävä nykyinen aika-arvo C on suurempi kuin 15 (lisäämme +1 aikaa yksinkertaisuuden). Toisin sanoen, Kun viesti saapuu ja vastaanottajan kello näyttää arvon, joka edeltää sitä aikaleimaa, joka osoittaa viestin lähdön, vastaanottaja siirtää kellonsa nopeasti eteenpäin siten, että se on yksi aikayksikkö enemmän kuin lähtöaika. Kuvassa 6 näemme, että m2 Korjaa nyt kellon arvon C: ssä arvoon 16. Vastaavasti m3 ja m4 ovat 30 ja 36.

edellä mainitusta esimerkistä Maarten van Steen et al muotoilee Lamportin algoritmin seuraavasti:

1. Ennen tapahtuman suorittamista (ts.viestin lähettäminen verkon kautta, …), pᵢ lisätään cᵢ: Cᵢ <- Cᵢ + 1.

2. Kun prosessi Pᵢ lähettää viestin m prosessille PJ, se asettaa m: n aikaleiman ts(m) yhtä suureksi kuin Cᵢ edellisen vaiheen suorittamisen jälkeen.

3. Saatuaan viestin m, prosessi Pj säätää oman paikallisen laskurin muodossa CJ <- max{Cj, ts(m)}, jonka jälkeen se suorittaa ensimmäisen vaiheen ja toimittaa viestin sovellukseen.

Vektorikellot

muista Lamportin määritelmä” tapahtuu-ennen ” – suhteesta, jos on kaksi tapahtumaa a ja b siten, että a esiintyy ennen b: tä, niin a on myös sijoitettu kyseiseen järjestykseen ennen b: tä, eli C(a) < C(b). Tämä ei kuitenkaan tarkoita käänteistä kausaliteettia, koska emme voi päätellä, että a menee B: n edelle pelkästään vertaamalla C(a): n ja C(b): n arvoja (todiste jää lukijan tehtäväksi).

jotta tapahtumien järjestämisestä saataisiin enemmän tietoa niiden aikaleiman perusteella, on ehdotettu Vektorikelloja, joka on kehittyneempi versio Lamportin loogisesta kellosta. Jokaiselle järjestelmän prosessille Pᵢ algoritmi ylläpitää vektoria VCᵢ, jolla on seuraavat attribuutit:

1. VCᵢ: paikallinen looginen kello pᵢ: ssä, tai niiden tapahtumien lukumäärä, jotka ovat tapahtuneet ennen nykyistä aikaleimaa.

2. Jos VCᵢ = k, pᵢ tietää, että k-tapahtumat ovat tapahtuneet PJ: llä.

vektorikellojen algoritmi menee tämän jälkeen seuraavasti:

1. Ennen tapahtuman toteuttamista Pᵢ kirjaa uuden tapahtuman tapahtuvan itsestään suorittamalla vcᵢ < – VCᵢ + 1.

2. Kun Pᵢ lähettää viestin m PJ: lle, se asettaa aikaleiman ts(m) yhtä suureksi kuin vcᵢ edellisen vaiheen suorittamisen jälkeen.

3. Kun viesti m on vastaanotettu, prosessi Pj päivittää jokaisen k Oman vektorikellonsa: vcj ← max { VCj, ts (m)}. Sitten se jatkaa ensimmäisen vaiheen suorittamista ja toimittaa viestin sovellukseen.

näiden vaiheiden kautta, kun prosessi Pj vastaanottaa viestin m prosessilta Pᵢ aikaleimalla ts (m), se tietää niiden tapahtumien määrän, jotka ovat tapahtuneet pᵢ: llä ohimennen m: n lähettämistä. lisäksi Pj tietää myös tapahtumista, jotka ovat olleet Pᵢ: n tiedossa muista prosesseista ennen m: n lähettämistä (kyllä se on totta, jos liittät tämän algoritmin Juoruprotokollaan🙂).

toivottavasti selitys ei jätä raapimaan päätä liian pitkäksi aikaa. Sukelletaan esimerkki hallita käsite:

tässä esimerkissä kolme prosessia P₁, P₂ ja P₃ vaihtoehtoisesti vaihtavat viestejä synkronoidakseen kellonsa yhteen. P₂ lähettää viestin M1 loogisena aikana VC₁ = (1, 0, 0) (Vaihe 1) P₂: lle. P↓, kun potilas saa M1: tä aikaleimalla ts(m1) = (1, 0, 0), muuttaa loogisen ajan VC₂-arvoksi (1, 1, 0) (Vaihe 3) ja lähettää viestin m2 takaisin P₁: lle aikaleimalla (1, 2, 0) (Vaihe 1). Vastaavasti prosessi p₂ hyväksyy p₂: n viestin m2, muuttaa loogisen kellonsa arvoon (2, 2, 0) (Vaihe 3), minkä jälkeen se lähettää viestin m3 arvoon P₃ at (3, 2, 0). P₃ säätää kellonsa (3, 2, 1) (Vaihe 1) sen jälkeen, kun se saa viestin m3 P₁: ltä. Myöhemmin se ottaa viestiin M4, jonka P tullaan lähettämään numerolla (1, 4, 0), ja siten säätää kellon arvoon (3, 4, 2) (Vaihe 3).

sen perusteella, miten nopeutamme sisäisiä kelloja synkronointia varten, tapahtuma a edeltää tapahtumaa B, jos kaikilla k, ts(a) ≤ ts(b), ja on ainakin yksi indeksi k’, jolle ts(a) < ts(b). Ei ole vaikea nähdä ,että (2, 2, 0) edeltää (3, 2, 1), mutta (1, 4, 0) ja (3, 2, 0) voivat olla ristiriidassa keskenään. Siksi vektorikelloilla voidaan havaita, onko minkä tahansa kahden tapahtuman välillä kausaalista riippuvuutta.

Take away

kun puhutaan ajan käsitteestä hajautetussa järjestelmässä, ensisijainen tavoite on saavuttaa tapahtumien oikea järjestys. Tapahtumat voidaan sijoittaa joko aikajärjestykseen fyysisillä kelloilla tai loogiseen järjestykseen Lamtportin loogisilla kelloilla ja Vektorikelloilla suoritusaikajanaa pitkin.

mitä seuraavaksi?

seuraavaksi sarjassa käydään läpi, miten aikasynkronointi voi tarjota yllättävän yksinkertaisia vastauksia joihinkin klassisiin ongelmiin hajautetuissa järjestelmissä: korkeintaan yksi viesti , välimuistin johdonmukaisuus ja molemminpuolinen poissulkeminen .

Leslie Lamport: Time, Clocks, and the order of Events in a Distributed System. 1978.

Barbara Liskov: synkronoitujen kellojen käytännön käyttötarkoitukset hajautetuissa järjestelmissä. 1993.

Maarten van Steen, Andrew S. Tanenbaum: Distributed Systems. 2017.

Barbara Liskov, Liuba Shrira, John Wroclawski: Tehokas korkeintaan kerran synkronoituihin kelloihin perustuvat viestit. 1991.

Cary G. Gray, David R. Cheriton: Leases: an Efficient Fault-tolerance Mechanism for Distributed File Cache Consistency. 1989.

Ricardo Gusella, Stefano Zatti: tempolla saavutettu kellon synkronoinnin tarkkuus Berkeley UNIX 4.3 BSD: ssä. 1989.