Complete metric space

matematiikassa kokonainen metrinen avaruus on metrinen avaruus, jossa jokainen Cauchyn sekvenssi on konvergentti. Toisin sanoen jokainen Cauchyn jono metrisessä avaruudessa pyrkii rajaan pisteeseen, joka on jälleen kyseisen avaruuden osa. Näin ollen metrinen avaruus on tavallaan ” täydellinen.”

• 1 formaali määritelmä
• 2 Examples
• 3 Completion
  • 3. 1 Examples
• 4 topologisesti täydellinen tila
• 5 Katso myös

formaali määritelmä

olkoon X metrinen avaruus metrisellä d: llä. silloin X on täydellinen, jos jokaiselle Cauchyn jaksolle 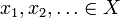on alkio 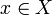sellainen, että .

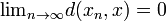esimerkit

• reaaliluvut R ja yleisemmin äärellisulotteiset Euklidiset avaruudet, joilla on tavanomainen metriikka, ovat täydellisiä.
• mikä tahansa kompakti metrinen avaruus on peräkkäisesti kompakti ja siten täydellinen. Converse ei pidä: esimerkiksi R on täydellinen, mutta ei kompakti.
• avaruudessa, jossa on diskreetti metriikka, ainoat Cauchyn sekvenssit ovat ne, jotka ovat vakioita jostakin pisteestä lähtien. Näin ollen mikä tahansa diskreetti metrinen avaruus on täydellinen. Näin ollen jotkut rajatut täydelliset metriset avaruudet eivät ole kompakteja.
• rationaaliluvut Q eivät ole täydellisiä. Esimerkiksi x0 = 1: n määrittelemä jono (xn), xn+1 = 1 + 1/xn on Cauchyn, mutta ei suppene Q: ssa (R: ssä se konvergoituu irrationaaliluvuksi.)

täydennys

jokaisella metrisellä avaruudella X on täydennys 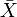, joka on kokonainen metrinen avaruus, johon X on isometrisesti upotettu tiheänä aliavaruutena. Valmistumisella on universaali ominaisuus.

esimerkit

• reaaliluvut R ovat rationaalilukujen Q täydennyksiä suhteessa tavalliseen absoluuttisen etäisyyden metriikkaan.

topologisesti täydellinen avaruus

täydellisyys ei ole topologinen ominaisuus: on mahdollista, että kokonainen metrinen avaruus on homeomorfinen sellaisen metrisen avaruuden kanssa, joka ei ole täydellinen. Esimerkiksi reaaliviiva R on homeomorfinen avoimen intervallin kanssa, vaikkapa (0,1). Toinen esimerkki: kartta

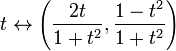
on homeomorfismi täydellisen metrisen avaruuden R ja epätäydellisen avaruuden välillä,joka on euklidisen tason yksikköympyrä, jonka piste (0, -1) on poistettu. Jälkimmäinen avaruus ei ole täydellinen, koska ei – Cauchyn sekvenssi, joka vastaa T=n, koska n kulkee positiivisten kokonaislukujen kautta, on kartoitettu ei-konvergentiksi Cauchyn sekvenssiksi ympyrällä.

voimme määritellä topologisen avaruuden metrisesti topologisesti täydelliseksi, jos se on homeomorfinen täydellisen metrisen avaruuden kanssa. Topologinen ehto tälle ominaisuudelle on, että avaruus on metrisoitavissa ja absoluuttinen Gδ eli gδ jokaisessa topologisessa avaruudessa, johon se voidaan upottaa (tai vain gδ sen täyttymisessä valitussa metriikassa). Erityisesti kaikki Euklidisten avaruuksien avoimet osajoukot ovat metrisesti topologisesti täydellisiä.

Katso myös

• Banachin avaruus
• Hilbertin avaruus

Osa tämän sivun sisällöstä on saattanut aiemmin ilmestyä Citizendium-sivustolle.