Johdonmukainen estimaattori: johdonmukaisuuden määrittely & esimerkit

tilastolliset määritelmät > johdonmukainen estimaattori

mikä on johdonmukainen estimaattori?

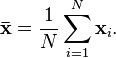
otoksen keskiarvo on populaation keskiarvon johdonmukainen estimaattori.

johdonmukaisessa arviossa on merkityksettömiä virheitä (vaihteluita) otoskokojen kasvaessa suuremmiksi. Tarkemmin sanottuna todennäköisyys, että nämä virheet vaihtelevat enemmän kuin tietty määrä, lähestyy nollaa otoksen koon kasvaessa. Toisin sanoen, Mitä enemmän tietoja keräät, johdonmukainen estimaattori on lähellä todellista populaatioparametria, jota yrität mitata. Otoksen keskiarvo ja otosvarianssi ovat kaksi tunnettua johdonmukaista estimaattoria.

johdonmukaisuuden ajatusta voidaan soveltaa myös mallivalintaan, jossa valitaan johdonmukaisesti “tosi” malli siihen liittyvine “tosi” – parametreineen. Johdonmukaisuuden mittana voidaan käyttää myös esimerkiksi hyvyystestiä (goodness of fit test). Yksi suosittu hyvyys fit testi on chi-neliö testi, joka toimii sillä edellytyksellä, että odotusarvot tietosi sopivat normaalijakauma. Ja jos sinulla on tietoja aikasarjamallista, datan johdonmukaisuutta voidaan mitata autoregressiivisellä mallilla. Monia muita johdonmukaisuuden mittareita tietojen sovittamiseksi malleihin on olemassa. Käyttämäsi menetelmä riippuu siitä, mitä haluat tietojesi mittaavan. Uskotko esimerkiksi, että tietosi seuraavat lineaarista trendiä, eksponentiaalista trendiä tai tiettyä trendiä, kuten tässä asiakirjassa, jossa esitetään johdonmukainen estimaattori rahoitusmallien häiriökomponenteille?

Origins

termi johdonmukainen estimaattori on lyhenne termistä” johdonmukainen estimaattorien sarja”, joka esiintyy käsitteessä convergence in probability. Perusajatus on, että toistat estimaattorin tulokset yhä uudelleen, tasaisesti kasvavilla otoskooilla. Lopulta-olettaen, että estimaattori on johdonmukainen — sekvenssi lähentyy todellisen populaatioparametrin. Tätä konvergenssia kutsutaan rajaksi, joka on calculuksen keskeinen rakennuspalikka.

Cramér, H. (1946). Mathematical methods of statistics”, Princeton Univ. Paina Sisäistä Tutkintaa. Ibragimov, R. Z. Has ‘ minskii, (1981) “Statistical estimation: asymptotic theory” , Springer.
Levinsohn, J. & MacKie-Mason, J. (1989). Yksinkertainen, cons. est. rahoitusmallien häiriökomponenttien osalta. National Bureau of Economic Research. Technical working paper No. 80. Viitattu 7. tammikuuta 2017 alkaen http://www.nber.org/papers/t0080.pdf.

——————————————————————————

Tarvitsetko apua kotitehtävissä tai koekysymyksessä? Chegg Studyn avulla saat askelmittaisia ratkaisuja kysymyksiisi alan asiantuntijalta. Ensimmäinen 30 minuuttia Chegg tutor on ilmainen!