terveyspisteet Cogs

by Posted on

Cogs on tietty määrä terveyspisteitä (HP) riippuen niiden tasosta. Tason 1 rattaissa on pienin hevosvoima, kun taas tason 12 rattaissa on suurin hevosvoima.

alla olevasta taulukosta käy ilmi, kuinka paljon HP: tä kullakin Ratastasolla on ja mitkä gagit voivat päihittää Rataksen yhdellä osumalla. Jotkut Pilat saattavat tarvita orgaanista.

taso terveyspisteet yhden hitin gagit
1 6 Leivos (6 vahinkoa)
kukkaruukku (10 vahinkoa)
vesilasi (6 vahinkoa)
2 12 Banaaninkuori (12 vahinkoa)
Vesipyssy (12 vahinkoa)
hiekkasäkki (18 vahinkoa)
3 20 Rake (20 vahinkoa)
Norsunrunko (21 vahinkoa)
Seltzer-pullo (21 vahinkoa)
4 30 paloletku (30 vahinkoa)
alasin (30 vahinkoa)
Kuula (35 vahinko)
5 42 iso paino (45 vahinkoa)
luomu koko kermapiirakka (44 vahinkoa)
juoksuhiekka (50 vahinkoa)
6 56 turvallinen (60 vahinkoa)
luukku (70 vahinkoa)
7 72 Organic Trapdoor (77 vahinkoa)
myrskypilvi (80 vahinkoa)
8 90 oopperalaulaja (90 vahinkoa)
syntymäpäiväkakku (100 vahinkoa)
9 110 orgaaninen syntymäpäiväkakku (110 vahinkoa)
orgaaninen Geysir (115 vahinko)
10 132 Luomuhääkakku (132 vahinkoa)
11 156 flyygeli (170 vahinkoa)
TNT (180 vahinkoa)
12 200 Luomurata (214 vahinkoa)

kaavat

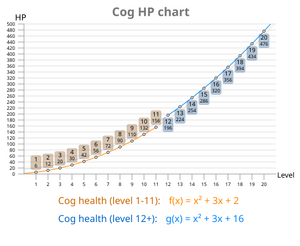
kaavio, joka näyttää rattaiden terveyden kasvun niiden tason mukaan. Ero 12-tason rattaiden terveydessä näkyy.

Rataksen terveyden kaava voi olla joko:

{\displaystyle f (x)=x^{2}+3x + 2}

tai yksinkertaistettuna:

{\displaystyle f(x)=(x+1)\times (x+2)}

missä x on Rataksen taso ja f (x) on funktio, joka palauttaa rattaiden terveysarvon.

esimerkiksi kaava toimii seuraavalla menetelmällä tason neljä rattaille, joiden teho on 30 hv:

{\displaystyle f(4)=(4+1)\ajat (4+2)} {\displaystyle f (4)=(5)\times (6)} {\displaystyle f(4)=30}

yllä oleva kaava koskee kaikkia Ratastasoja paitsi tasoa 12,jossa on 200 hv.

jotta voidaan hakea Rataksen taso annetusta HP: sta sen sijaan, että haettaisiin HP tasolta, voidaan käyttää kvadraattista kaavaa, jossa n on HP:

{\displaystyle x_{1,2}={\frac {-3 \ pm {\sqrt {9-4 * (2-n)}}}{2}}}

yhtälö ratkeaa esimerkiksi seuraavalla menetelmällä, jolla saadaan selville, kummalla Ratasella olisi 156 hv:

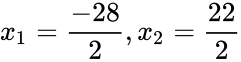
{\displaystyle x_{1,2}={\frac {-3 \ pm {\sqrt {9-4*(2-156)}}}{2}}} {\displaystyle x_{1,2}={\frac {-3 \ pm {\sqrt {9-4*-154}}}{2}}} {\displaystyle x_{1,2}={\frac {-3 \ pm {\sqrt {9+616}}}{2}}} {\displaystyle x_{1,2}={\frac {-3 \ pm {\sqrt {625}}}{2}}} {\displaystyle x_{1,2} = {\frac {-3 \ pm 25}{2}}} {\displaystyle x_{1} = {\frac {-3-25}{2}},x_{2} = {\frac {-3+25}{2}}} {\displaystyle x_{1}={\frac {-28}{2}}, x_{2} = {\frac {22}{2}}} {\displaystyle x_{1}=-14, x_{2}=11}

koska f (x) on paraabelin funktio eikä yksikään ratkaisuista ole funktion minimiarvo, yhtälölle on kaksi vastausta: -14, joka ei ole todellinen Ratastaso, ja 11, joka on todellinen taso.

vaikka tämä kaava toimii kaikilla Ratastasoilla, kun se ylittää säännölliset Ratastasot, tämä kaava alkaa olla käytännössä soveltumaton kompleksilukujen vuoksi. Jos n arvo on alle -0,25, tämä yhtälö esittelee kompleksilukuja, jotka toimivat edelleen teoriassa mutta eivät käytännössä.

Trivia

  • vaikka tason 12 rattaissa pitäisi olla 182 hv, niissä sen sijaan on 200, mikä on käytännössä 10%: n boost. Kaavan mukaan, Ratas 200 hv pitäisi olla noin tasolla 12.65 (tai noin -15.65, vaikka negatiiviset arvot eivät ole yhteensopivia Cog tasot).
  • kaavan mukaan Väijytysmarkkinoinnin johtajalla olisi 2 652 hevosvoimaa, koska se on tasoa 50.

Published by admin

Vastaa

Sähköpostiosoitettasi ei julkaista.