Gesundheitspunkte von Zahnrädern / Toontown Rewritten Wiki

Zahnräder haben eine bestimmte Anzahl von Gesundheitspunkten (HP), abhängig von ihrem Level. Stufe 1 Zahnräder haben die niedrigste Menge an HP, während Stufe 12 Zahnräder haben die höchste Menge an HP.

Die folgende Tabelle zeigt, wie viel HP jede Zahnradstufe hat und welche Gags das Zahnrad mit einem Treffer besiegen können. Einige Gags müssen möglicherweise organisch sein.

Stufe	Lebenspunkte	One-Hit-Gags
1	6	Cupcake (6 Schaden) Blumentopf (10 Schaden) Glas Wasser (6 Schaden)
2	12	Bananenschale (12 Schaden) Spritzpistole (12 Schaden) Sandsack (18 Schaden)
3	20	Rechen (20 Schaden) Elefantenrüssel (21 Schaden) Selterflasche (21 Schaden)
4	30	Feuerwehrschlauch (30 Schaden) Amboss (30 Schaden) Murmeln (35 schaden)
5	42	Großes Gewicht (45 Schaden) Organische ganze Sahnetorte (44 Schaden) Treibsand (50 Schaden)
6	56	Sicher (60 Schaden) Falltür (70 Schaden)
7	72	Organische Falltür (77 Schaden) Gewitterwolke (80 Schaden)
8	90	Opernsänger (90 Schaden) Geburtstagstorte (100 Schaden)
9	110	Bio-Geburtstagstorte (110 Schaden) Bio-Geysir (115 schaden)
10	132	Bio Hochzeitstorte (132 ))
11	156	Flügel (170 Schaden) TNT (180 Schaden)
12	200	Bio-Baumwolle (214))

Formeln

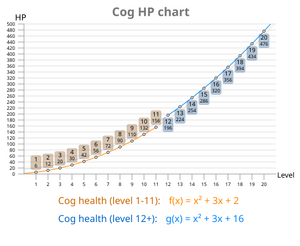
Eine Grafik, die das Gesundheitswachstum von Zahnrädern nach ihrem Niveau zeigt. Der Unterschied in der Gesundheit von Zahnrädern der Stufe 12 ist zu sehen.

Die Formel für die Gesundheit eines Zahnrads kann entweder sein:

$f(x)=x^{2}+3x+2$

oder vereinfacht ausgedrückt:

$f(x)=(x+1)\times (x+2)$

wobei x der Pegel des Zahnrads ist und f (x) eine Funktion ist, die den Integritätswert von Zahnrädern zurückgibt.

Zum Beispiel funktioniert die Formel in der folgenden Methode für Level vier Zahnräder, die 30 PS haben:

$f(4)=(4+1)\ zeiten (4+2)$ ${\ displaystyle f(4)=(5)\Zeiten (6)}$ ${\ displaystyle f(4)=30}$

Die obige Formel gilt für jede Zahnradstufe außer Stufe 12, die 200 PS hat.

Um den Level des Zahnrads von einer gegebenen HP abzurufen, anstatt die HP von der Ebene abzurufen, kann eine quadratische Formel verwendet werden, wobei n die HP ist:

$x_{1,2}={\frac {-3\pm {\sqrt {9-4*(2-n)}}}{2}}$

Zum Beispiel wird die Gleichung in der folgenden Methode gelöst, um herauszufinden, welches Zahnrad 156 PS haben würde:

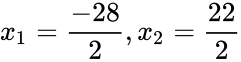
$x_{1,2}={\frac {-3\pm {\sqrt {9-4*(2-156)}}}{2}}$ ${\ displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9-4*-154}}}{2}}}$ ${\ displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9+616}}}{2}}}$ ${\ displaystyle x_{1,2}={\frac {-3\pm {\sqrt {625}}}{2}}}$ ${\ displaystyle x_{1,2}={\frac {-3\pm 25}{2}}}$ ${\ displaystyle x_{1}={\frac {-3-25}{2}}, x_{2}={\frac {-3+25}{2}}}$ ${\ displaystyle x_{1}={\frac {-28}{2}},x_{2}={\frac {22}{2}}}$ ${\ displaystyle x_{1}=-14,x_{2}=11}$

Da f (x) eine Funktion einer Parabel ist und keine der Lösungen ist der Minimalwert der Funktion, es gibt zwei Antworten für die Gleichung: -14, was kein echtes Zahnradniveau ist; und 11, was ein reales Niveau ist.

Obwohl diese Formel für alle Zahnradstufen funktioniert, ist diese Formel in der Praxis aufgrund komplexer Zahlen nicht anwendbar, wenn sie über die regulären Zahnradstufen hinausgeht. Für jeden n-Wert kleiner als -0,25 führt diese Gleichung komplexe Zahlen ein, die in der Theorie immer noch funktionieren, aber in der Praxis nicht.

Obwohl Level 12 Zahnräder 182 PS haben sollten, haben sie stattdessen 200, was im Wesentlichen ein 10% iger Schub ist. Gemäß der Formel sollte ein Zahnrad mit 200 PS etwa Stufe 12,65 betragen (oder etwa -15,65, obwohl negative Werte nicht mit Zahnradstufen kompatibel sind).

Gemäß der Formel hätte der Direktor für Hinterhaltmarketing 2.652 PS, da es sich um Stufe 50 handelt.

Gesundheitspunkte von Zahnrädern

Formeln

Published by admin

Schreibe einen Kommentar Antworten abbrechen