Glasfaser-Tutorial – Glasfaser – Kommunikationsfaser

Grundbegriffe

Lichtbrechung

Wenn ein Lichtstrahl von einem transparenten Medium zum anderen gelangt, ändert er die Richtung; Dieses Phänomen wird Lichtbrechung genannt. Wie stark dieser Lichtstrahl seine Richtung ändert, hängt vom Brechungsindex der Medien ab.

Brechungsindex

Brechungsindex ist die Lichtgeschwindigkeit im Vakuum (abgekürzt c, c=299.792.458km/Sekunde) geteilt durch die Lichtgeschwindigkeit in einem Material (abgekürzt v). Der Brechungsindex misst, wie stark ein Material Licht bricht. Der Brechungsindex eines Materials, abgekürzt als n, ist definiert als

n= c / v

Snells Gesetz

1621 leitete ein niederländischer Physiker namens Willebrord Snell die Beziehung zwischen den verschiedenen Lichtwinkeln ab, die von einem transparenten Medium zum anderen gelangen. Wenn Licht von einem transparenten Material zu einem anderen gelangt, biegt es sich nach dem Snellschen Gesetz, das definiert ist als:

n1sin(θ1) = n2sin(θ2)

wobei:
n1 der Brechungsindex des Mediums ist, das das Licht verlässt
θ1 ist der Einfallswinkel zwischen dem Lichtstrahl und der Normalen (normal ist 90 ° zur Grenzfläche zwischen zwei Materialien)
n2 ist der Brechungsindex des Materials, in das das Licht eintritt
θ2 ist der Brechungswinkel des zwischen dem Lichtstrahl und der Normalen

Hinweis:

Für den Fall von θ1 = 0 ° (d. h. ein Strahl senkrecht zur Grenzfläche) ist die Lösung θ2 = 0 ° unabhängig von den Werten von n1 und n2. Das bedeutet, dass ein Strahl, der senkrecht zur Oberfläche in ein Medium eintritt, niemals gebogen wird.

Das Obige gilt auch für Licht, das von einem dichten (höheres n) zu einem weniger dichten (niedrigeres n) Material geht; Die Symmetrie des Snellschen Gesetzes zeigt, dass die gleichen Strahlengänge in entgegengesetzter Richtung anwendbar sind.

Interne Totalreflexion

Wenn ein Lichtstrahl eine Grenzfläche in ein Medium mit einem höheren Brechungsindex kreuzt, biegt er sich zur Normalen. Umgekehrt biegt sich Licht, das eine Grenzfläche von einem Medium mit höherem Brechungsindex zu einem Medium mit niedrigerem Brechungsindex durchquert, von der Normalen weg.

Dies hat eine interessante Implikation: In einem Winkel, der als kritischer Winkel θc bekannt ist, wird Licht, das von einem Medium mit höherem Brechungsindex zu einem Medium mit niedrigerem Brechungsindex wandert, bei 90 ° gebrochen; mit anderen Worten, entlang der Grenzfläche gebrochen.

Wenn das Licht in einem Winkel, der größer als dieser kritische Winkel ist, auf die Grenzfläche trifft, gelangt es überhaupt nicht zum zweiten Medium. Stattdessen wird alles zurück in das erste Medium reflektiert, ein Prozess, der als totale interne Reflexion bekannt ist.

Der kritische Winkel kann aus dem Snellschen Gesetz berechnet werden, wobei für den Winkel des gebrochenen Strahls θ2 ein Winkel von 90 ° angegeben wird. Dies ergibt θ1:

Seit

θ2 = 90°

Also

sin(θ2) = 1

Dann

θc = θ1 = arcsin(n2/n1)

Zum Beispiel, wenn Licht versucht, aus Glas mit n1 = 1,5 in Luft (n2 = 1) auszutreten, beträgt der kritische Winkel θc arcsin (1/1,5) oder 41,8 °.

Für jeden Einfallswinkel, der größer als der kritische Winkel ist, kann das Snellsche Gesetz für den Brechungswinkel nicht gelöst werden, da es zeigt, dass der gebrochene Winkel einen Sinus größer als 1 hat, was nicht möglich ist. In diesem Fall wird das gesamte Licht vollständig von der Grenzfläche reflektiert, wobei das Gesetz der Reflexion befolgt wird.

Funktionsweise optischer Fasern

Optische Fasern basieren vollständig auf dem Prinzip der Totalreflexion. Dies wird in der folgenden Abbildung erläutert.

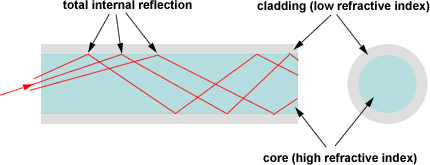
Glasfaser ist ein langer, dünner Strang aus sehr reinem Glas mit dem Durchmesser eines menschlichen Haares. Optische Fasern sind in Bündeln angeordnet, die als optische Kabel bezeichnet werden und zur Übertragung von Lichtsignalen über große Entfernungen verwendet werden.

Die Struktur einer optischen Faser

Typische optische Fasern bestehen aus Kern, Mantel und Pufferbeschichtung.

Der Kern ist der innere Teil der Faser, der das Licht leitet. Der Mantel umgibt den Kern vollständig. Der Brechungsindex des Kerns ist höher als der des Mantels, so dass Licht im Kern, das in einem Winkel, der flacher als der kritische Winkel ist, auf die Grenze zum Mantel trifft, durch Totalreflexion in den Kern zurückreflektiert wird.

Für die gängigsten optischen Glasfasertypen, zu denen 1550-nm-Singlemode-Fasern und 850-nm- oder 1300-nm-Multimode-Fasern gehören, reicht der Kerndurchmesser von 8 bis 62,5 µm. Der gebräuchlichste Manteldurchmesser beträgt 125 µm. Das Material der Pufferbeschichtung ist normalerweise weicher oder harter Kunststoff wie Acryl, Nylon und mit einem Durchmesser von 250 µm bis 900 µm. Die Pufferbeschichtung bietet mechanischen Schutz und Biegeflexibilität für die Faser.

Optischer Fasermodus

Was ist Fasermodus?

Eine optische Faser leitet Lichtwellen in verschiedenen Mustern, die als Moden bezeichnet werden. Mode beschreibt die Verteilung der Lichtenergie über die Faser. Die genauen Muster hängen von der Wellenlänge des übertragenen Lichts und von der Variation des Brechungsindex ab, der den Kern formt. Im Wesentlichen schaffen die Variationen des Brechungsindex Randbedingungen, die bestimmen, wie sich Lichtwellen durch die Faser bewegen, wie die Wände eines Tunnels beeinflussen, wie Geräusche im Inneren widerhallen.

Wir können einen Blick auf Step-Index-Fasern mit großem Kern werfen. Lichtstrahlen treten in einer Reihe von Winkeln in die Faser ein, und Strahlen in verschiedenen Winkeln können sich alle stabil über die Länge der Faser erstrecken, solange sie die Kern-Mantel-Grenzfläche in einem Winkel treffen, der größer als der kritische Winkel ist. Diese Strahlen sind verschiedene Modi.

Fasern, die mehr als eine Mode bei einer bestimmten Lichtwellenlänge tragen, werden Multimode-Fasern genannt. Einige Fasern haben einen Kern mit sehr kleinem Durchmesser, so dass sie nur einen Modus tragen können, der sich als gerade Linie in der Mitte des Kerns bewegt. Diese Fasern sind Monomode-Fasern. Dies ist in der folgenden Abbildung dargestellt.

Optisches Faserindexprofil

Indexprofil ist die Brechungsindexverteilung über den Kern und die Umhüllung einer Faser. Einige optische Fasern haben ein Stufenindexprofil, bei dem der Kern einen gleichmäßig verteilten Index und der Mantel einen niedrigeren gleichmäßig verteilten Index aufweist. Andere optische Fasern haben ein abgestuftes Indexprofil, bei dem der Brechungsindex allmählich als Funktion des radialen Abstands von der Fasermitte variiert. Graded-Index-Profile umfassen Potenzgesetz-Indexprofile und parabolische Indexprofile. Die folgende Abbildung zeigt einige gängige Arten von Indexprofilen für Singlemode- und Multimode-Fasern.

Optische Faser der Numerische Apertur (NA)

Multimode optische faser wird nur propagieren licht, dass tritt die faser innerhalb einer bestimmten kegel, bekannt als die akzeptanz kegel der faser. Der Halbwinkel dieses Kegels wird als Akzeptanzwinkel θmax bezeichnet. Bei Step-Index-Multimode-Fasern wird der Akzeptanzwinkel nur durch die Brechungsindizes bestimmt:

Wobei
n der Brechungsindex des Mediums ist, das sich vor dem Eintritt in die Faser bewegt
nf ist der Brechungsindex des Faserkerns
nc ist der Brechungsindex der Umhüllung

Wie berechnet man die Anzahl der Modi in einer Faser?

Modi sind manchmal durch Zahlen gekennzeichnet. Singlemode-Fasern tragen nur den Modus niedrigster Ordnung, dem die Nummer 0 zugewiesen ist. Multimode-Fasern tragen auch Modi höherer Ordnung. Die Anzahl der Moden, die sich in einer Faser ausbreiten können, hängt von der numerischen Apertur (oder dem Akzeptanzwinkel) der Faser sowie von ihrem Kerndurchmesser und der Wellenlänge des Lichts ab. Für eine Step-Index-Multimode-Faser wird die Anzahl solcher Moden, Nm, angenähert durch

Wobei
D der Kerndurchmesser ist
λ ist die Betriebswellenlänge
NA ist die numerische Apertur (oder der Akzeptanzwinkel)

Hinweis: Diese Formel ist nur eine Näherung und funktioniert nicht für Fasern, die nur ein paar Modi.