4.1: Kinetic Energy
kinetikus energia ütközésekben
ahhoz, hogy további betekintést nyerjünk a kinetikus energia fogalmába, és hogy milyen módon különbözik a momentumtól, hasznos, ha ugyanabban a környezetben vizsgáljuk, amelyben “felfedeztük” a Momentumot, nevezetesen egydimenziós ütközéseket egy elszigetelt rendszerben. Ha megnézzük újra az ütközés ábrán látható 3.1.1 Fejezet 3, reprodukálni alább,
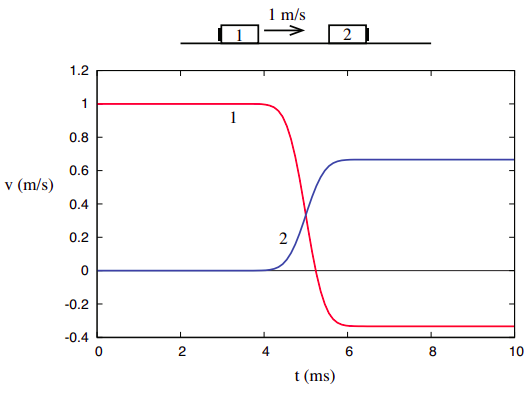
\
vegye figyelembe, hogy 1/18 + 4/9 = 9/18 = 1/2, és így
\
szavakban azt találjuk, hogy ebben az ütközésben a teljes kinetikus energia végső értéke megegyezik a kezdeti értékével, ezért úgy tűnik, hogy egy másik konzervált mennyiséget “fedeztünk fel” (a lendület mellett) ehhez a rendszerhez.
ezt a hitet megerősíthetjük, ha a következőkben a 3. fejezet 3.1.2. ábráján ábrázolt ütközést vizsgáljuk, amelyet az alábbiakban ismét megismételünk. Emlékezzünk arra, hogy akkoriban rámutattam, hogy ez valóban ugyanaz az ütközés, mint a 3.1.ábrán látható.1, csak nézett egy másik referenciakeret (egy mozgó kezdetben jobbra 1 m/s). A fejezet végére többet kell mondanunk arról, hogyan lehet a mennyiségeket referenciakeretről másikra átalakítani.
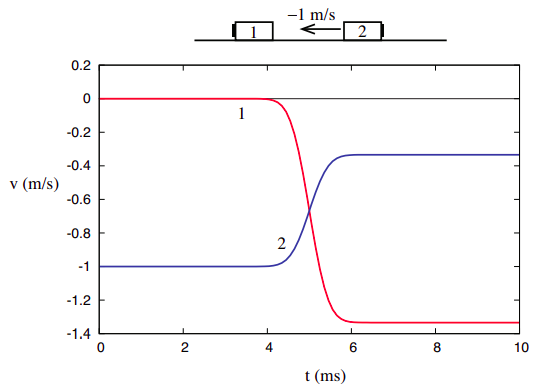
a dolgok azonban nagyon különbözőek, ha figyelembe vesszük a 3. fejezetben bemutatott harmadik ütközési példát, nevezetesen azt, amikor a két tárgy össze van ragadva az ütközés után.
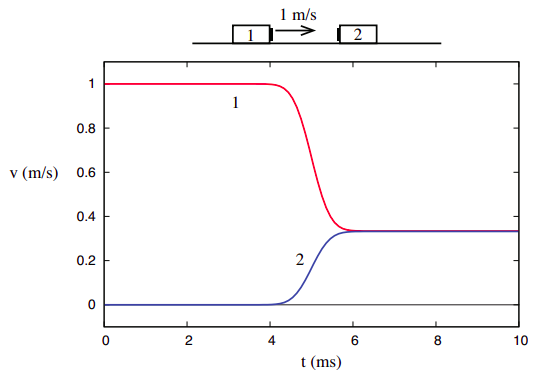
\
ez azonban azt mutatja, hogy a rendszer teljes lendületétől eltérően, amelyet a belső kölcsönhatások teljesen nem befolyásolnak, a teljes kinetikus energia az interakció részleteitől függ, és így bizonyos információkat közvetít a természetéről. Ezután finomíthatjuk az ütközések tanulmányozását, hogy megkülönböztessünk két fajtát: azokat, ahol az ütközés után a kezdeti kinetikus energia visszanyeri, amit rugalmasnak nevezünk, és azokat, ahol nem, amelyeket rugalmatlannak nevezünk. A rugalmatlan ütközés speciális esete az úgynevezett teljesen rugalmatlan, ahol a két tárgy végül összeragad, mint az ábrán \(\PageIndex{3}\). Mint később látni fogjuk, a kinetikus energia “hiánya” ebben az esetben a legnagyobb.
fentebb már említettem, hogy egy rugalmas ütközés során a kinetikus energia “visszanyerhető”, és ezt a terminológiát inkább a” konzervált ” helyett szeretem, mert valójában a teljes lendülettel ellentétben a rendszer teljes kinetikus energiája nem marad állandó az interakció során, még egy rugalmas ütközés során sem. A legegyszerűbb példa ennek bemutatására egy rugalmas, frontális ütközés két azonos tömegű tárgy között, azonos sebességgel haladva egymás felé. Az ütközés során mindkét tárgyat egy pillanatra megállítják, mielőtt visszafordulnának és visszapattannának, és ebben a pillanatban a teljes mozgási energia nulla.
megvizsgálhatja a fenti \(\PageIndex{1}\) és \(\PageIndex{2}\) ábrákat is, és a grafikonokból kiszámíthatja az ütközés során a teljes kinetikus energia értékét. Látni fogja, hogy minimálisra csökken, majd visszatér a kezdeti értékéhez (Lásd még a \(\PageIndex{4}\) ábrát, később ebben a fejezetben). Hagyományosan a kinetikus energiáról úgy beszélhetünk, hogy “konzervált” a rugalmas ütközésekben, de fontos felismerni, hogy másfajta “megőrzésre” van szükségünk, mint ami a teljes lendülettel volt, amely állandó volt az interakció előtt, alatt és után, mindaddig, amíg a rendszer elszigetelt maradt.
a rugalmas ütközések azt sugallják, hogy bármi legyen is ennek az “energiának” nevezett dolognak a végső természete, lehetséges, hogy valamilyen formában (ebben az esetben az ütközés során) tárolhatjuk, majd végül kinetikus energiaként visszanyerhetjük. Ez előkészíti az utat a mozgási energián kívül másfajta “energia” bevezetéséhez, amint azt egy későbbi fejezetben látni fogjuk, és az ilyen típusú átalakítások lehetőségét. Pillanatnyilag egyszerűen azt kell mondanunk, hogy egy elasztikus ütközés során bizonyos mennyiségű kinetikus energia ideiglenesen tárolódik valamiféle “belső energiaként”, és az ütközés után ez visszaalakul kinetikus energiává; míg egy rugalmatlan ütközés esetén bizonyos mennyiségű kinetikus energia visszavonhatatlanul átalakul valamilyen” belső energiává”, és soha nem kapjuk vissza.
mivel bármi is történik, az az interakció részleteitől és természetétől függ, különbséget kell tennünk a “konzervatív” kölcsönhatások között, ahol a kinetikus energia reverzibilisen tárolódik valahol valamilyen más energiaformaként, és a “disszipatív” kölcsönhatások között, ahol az energiaátalakítás legalább részben visszafordíthatatlan. Nyilvánvaló, hogy a rugalmas ütközések konzervatív kölcsönhatásokkal, az inelasztikus ütközések pedig disszipatív kölcsönhatásokkal járnak. Az interakciók ezen előzetes osztályozását azonban kissé alaposabban felül kell vizsgálni a következő fejezetben.