Energiaveszteség kapcsolókban
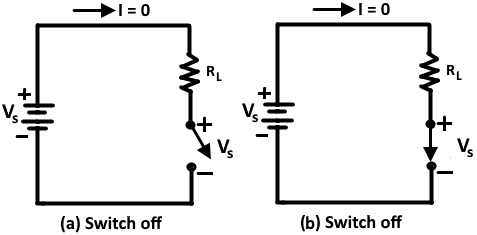
az ideális kapcsolót az 1. ábra mutatja. A kapcsolóban keletkező energiaveszteség a kapcsolón keresztüli áram és a kapcsolón keresztüli feszültség szorzata. Ha a kapcsoló ki van kapcsolva, nincs áram rajta keresztül (bár van feszültség VS rajta). Ezért nincs áramelosztás. Amikor a kapcsoló be van kapcsolva, áram (VS / RL) van rajta keresztül, de nincs feszültségesés rajta, tehát ismét nincs áramveszteség. Azt is feltételezzük, hogy ideális kapcsoló esetén az áram emelkedési és esési ideje nulla. Ez azt jelenti, hogy az ideális kapcsoló a kikapcsolt állapotról a bekapcsolt állapotra (és fordítva) azonnal változik. A kapcsolás közbeni energiaveszteség tehát nulla.
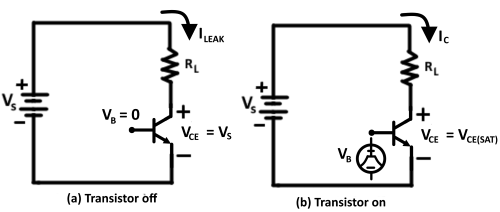
az ideális kapcsolóval ellentétben a tényleges kapcsolónak, például a bipoláris csatlakozási tranzisztornak két fő áramforrása van: vezetési veszteség és kapcsolási veszteség.
vezetési veszteség
amikor a 2.ábra(a) tranzisztor ki van kapcsolva, szivárgási áramot (lLEAK) hordoz. A szivárgási áramhoz kapcsolódó energiaveszteség POFF = VS x ILEAK . Mivel azonban a szivárgási áram meglehetősen kicsi, és nem változik jelentősen a feszültséggel, általában elhanyagolják, így a tranzisztor teljesítményvesztesége lényegében nulla. Amikor a tranzisztor be van kapcsolva, mint a 2(b) ábrán, kis feszültségesés van rajta. Ezt a feszültséget telítettségi feszültségnek (VCE(SAT)) nevezzük. A tranzisztor teljesítményeloszlása vagy vezetési vesztesége a telítettségi feszültség miatt:
PON = VCE(SAT) x IC
ahol
IC = (VS – VCE(SAT)) / RL vs / RL
az 1.egyenlet megadja a vezetőképesség miatti áramveszteséget, ha a kapcsoló határozatlan ideig bekapcsolva marad. Egy adott alkalmazás áramellátásának vezérléséhez azonban a kapcsolót rendszeresen ki-be kapcsolják. Ezért a feszültségveszteség megállapításához figyelembe kell vennünk a munkaciklust:
PON(avg) = VCE(SAT) x Ic x (ION / T) = VCE(SAT) x IC x d
hasonlóképpen
POFF(avg) = VS X ILEAK x tOFF / T
itt a D munkaciklus a ciklus százalékos aránya, amelyben a kapcsoló be van kapcsolva:
d = ton / (ton x toff ) = ton / t
kapcsolási veszteség
a vezetési veszteség mellett egy valódi kapcsolónak kapcsolási vesztesége van, mert nem tud azonnal bekapcsolt állapotból kikapcsolt állapotba (vagy fordítva) váltani. A valódi kapcsolónak véges időre van szüksége a tSW (ON)bekapcsolásához, és egy véges időre a tSW(OFF) kikapcsolásához. Ezek az idők nemcsak az energiaeloszlást vezetik be, hanem a lehető legmagasabb kapcsolási frekvenciát is korlátozzák. A tSW(ON) és tSW(OFF)átmeneti idők a valódi kapcsolók esetében általában nem egyenlőek, a tSW(ON) általában nagyobb. Ebben a vitában azonban feltételezzük, hogy a tSW(be) egyenlő a tSW-vel(ki). 3. ábra. Megmutatja a kapcsolási hullámformákat (a) a kapcsolón keresztüli feszültségre és (b) a rajta áthaladó áramra. Ha a kapcsoló ki van kapcsolva, a rajta lévő feszültség megegyezik a forrásfeszültséggel. A bekapcsolás során, amely véges időt vesz igénybe, a kapcsoló feszültsége nullára csökken. Ugyanakkor a kapcsolón keresztüli áram nulláról IC-re növekszik. A tranzisztornak áram van rajta, és feszültség van rajta a kapcsolási idő alatt; ezért energiavesztesége van.

ahhoz, hogy megtaláljuk a tranzisztorban a kapcsolási intervallum alatt eloszlatott teljesítményt, megszorozzuk az IC pillanatnyi értékét és a VCE megfelelő értékét. a pillanatnyi teljesítménygörbét a 3(c) ábra mutatja. a kapcsolóban eloszlatott energia megegyezik a teljesítményhullám alatti területtel. Vegye figyelembe, hogy a maximális teljesítmény eloszlik, ha mind az áram, mind a feszültség áthalad a középpont értékein. Ezért a maximális teljesítményveszteség kikapcsolt állapotról bekapcsolt állapotra váltáskor:
PSW be(max) = 0,5 VCE(max) x 0.5 IC (max)
érdekes megjegyezni, hogy a teljesítménygörbe lényegében úgy néz ki, mint egy korrigált szinuszhullám. Ennek a hullámformának az átlagos értéke
PSW be (avg) = 0,637 x PSW be (max)
= 0,637 x 0,5 VCE (MAX) x 0,5 IC (MAX)
= 0.167 VCE(max) x IC(max)
vagy
PSW be(avg) = 1/6 VCE(max) x IC(max)
az energiaveszteség (teljesítmény x idő) Bekapcsolás közben PSW be(avg) x tSW(ON)
WSW be = 1/6 VCE(max) x IC(max) x TSW(on) (Joule)
egy hasonló elemzés megadja az energiaveszteséget a kikapcsolás során, mint
WSW off = 1/6 VCE(max) x IC(max) x TSW(on) (Joule)
a kapcsolás miatti teljes energiaveszteséget
WSW = WSW on + WSW off + 1/6 VCE(max) X IC(max) x
a kapcsoló átlagos teljesítményeloszlása
PSW = WSW/t = WSW x f
PSW = 1/6 VCE(max) x IC(max) x F
ahol T a kapcsolási periódus, f pedig az impulzus ismétlési sebessége (a kapcsolás gyakorisága). Vegye figyelembe, hogy
T = tonna + tSW(be) + tOFF + tSW(ki)
ha hagyjuk
tSW(be) = tSW(be) tSW(ki) = tSW
akkor
PSW = 1/6 VCE(max) x IC(max) x (2 tSW) X F
a kapcsoló teljes energiavesztesége
pt = pon(átlag) + Poff(átlag) + PSW
fő(átlag) + PSW
= d x VCE(Szo) x IC 1/3 x VCE(max) x IC(Max) X TSW x f
dióda
fő értékelés diódák
dióda áramkör analízis
feszültség jelenlegi jellemző dióda
kialakulását kimerülése réteg dióda
alagút Dióda