időszinkronizálás elosztott rendszerekben

ha úgy találja magát ismeri weboldalak, mint facebook.com vagy a google.val vel, talán nem kevesebb, mint egyszer elgondolkodott azon, hogy ezek a webhelyek hogyan képesek másodpercenként millió vagy akár tízmillió kérést kezelni. Lesz-e egyetlen kereskedelmi szerver, amely képes ellenállni ennek a hatalmas kérésnek, abban a módon, hogy minden kérést időben kiszolgálni lehet a végfelhasználók számára?

mélyebben belemerülve ebbe a kérdésbe, eljutunk az elosztott rendszerek fogalmához, független számítógépek (vagy csomópontok) gyűjteményéhez, amelyek a felhasználók számára egyetlen koherens rendszerként jelennek meg. A felhasználók koherenciájának ez a fogalma egyértelmű, mivel úgy vélik, hogy egyetlen humongous géppel foglalkoznak, amely több, párhuzamosan futó folyamat formájában jelenik meg, hogy egyszerre kezelje a kérések tételeit. Azonban azok számára, akik megértik a rendszer infrastruktúráját, a dolgok nem olyan egyszerűek, mint ilyenek.

több ezer egyidejűleg futó független gép esetében, amelyek több időzónát és kontinenst is lefedhetnek, bizonyos típusú szinkronizálást vagy koordinációt kell biztosítani ahhoz, hogy ezek a gépek hatékonyan együttműködjenek egymással (hogy egyként jelenjenek meg). Ebben a blogban megvitatjuk az idő szinkronizálását és azt, hogy miként érhető el a gépek közötti következetesség az események rendezésében és okozati összefüggésében.

a blog tartalma a következőképpen szerveződik:

1. óra szinkronizálás
2. logikai órák
3. elvenni
4. mi a következő lépés?

fizikai órák

központosított rendszerben az idő egyértelmű. Szinte minden számítógép rendelkezik “valós idejű órával” az idő nyomon követésére, általában szinkronban egy pontosan megmunkált kvarckristálysal. Ennek a kvarcnak a jól meghatározott frekvencia-oszcillációja alapján a számítógép operációs rendszere pontosan figyelemmel kísérheti a belső időt. Még akkor is, ha a számítógépet kikapcsolják vagy lemerülnek, a kvarc továbbra is ketyeg a CMOS akkumulátor, az alaplapba integrált kis erőmű miatt. Amikor a számítógép csatlakozik a hálózathoz (Internet), az operációs rendszer ezután kapcsolatba lép egy időzítőkiszolgálóval, amely UTC vevővel vagy pontos órával van felszerelve, hogy pontosan visszaállítsa a helyi időzítőt a Network Time Protocol, más néven NTP segítségével.

bár a kristálykvarcnak ez a frekvenciája meglehetősen stabil, lehetetlen garantálni, hogy a különböző számítógépek összes kristálya pontosan ugyanazon a frekvencián fog működni. Képzeljünk el egy rendszert n számítógéppel, amelynek minden kristálya kissé eltérő sebességgel fut, aminek következtében az órák fokozatosan kikerülnek a szinkronból,és a kiolvasáskor különböző értékeket adnak. Az időértékek közötti különbséget az óra ferdeségének nevezzük.

ilyen körülmények között a dolgok rendetlenné váltak, mert több térben elválasztott gép volt. Ha kívánatos több belső fizikai óra használata, hogyan szinkronizálhatjuk őket a valós órákkal? Hogyan szinkronizáljuk őket egymással?

Network Time Protocol

a számítógépek közötti páronkénti szinkronizálás általános megközelítése az ügyfél-kiszolgáló modell használata, azaz az ügyfelek kapcsolatba lépése egy időszerverrel. Tekintsük a következő példát 2 A és B géppel:

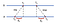
először is, A küld egy kérést időbélyeggel érték TL A B. B, ahogy az üzenet megérkezik, rögzíti a beérkezés idejét a saját helyi órájáról, és a válaszokat egy t₂-val bélyegzett üzenettel rögzíti, a korábban rögzített értéket a TNP-vel. Végül, A, Miután megkapta a választ B-től, rögzíti az érkezési időt TFC. A számlát a meghatározott idő elteltével az üzeneteket, úgy számoljuk, Δ₁ = T₁-T₀, Δ₂ = T₃-T₂. Most, a relatív B becsült eltolása az:

A (Z) A órajelét vagy lelassíthatjuk, vagy rögzíthetjük úgy, hogy a két gép szinkronizálható legyen egymással.

mivel az NTP páronként alkalmazható, B órája beállítható az a órájához is. Bölcs dolog azonban az órát B-ben beállítani, ha ismert, hogy pontosabb. A probléma megoldására, az NTP rétegekre osztja a szervereket, azaz rangsorolja a szervereket úgy, hogy a kevésbé pontos, kisebb rangú szerverek órái szinkronizálódjanak a magasabb rangú pontosabbakéval.

Berkeley algoritmus

ellentétben azokkal a kliensekkel, amelyek rendszeresen kapcsolatba lépnek egy időszerverrel a pontos időszinkronizálás érdekében, Gusella és Zatti 1989-ben a Berkeley Unix paper-ben javasolta a kliens-szerver modellt , amelyben az időszerver (démon) rendszeresen lekérdezi az összes gépet, hogy megkérdezze, mennyi az idő. A válaszok alapján kiszámítja az üzenetek oda-vissza idejét, átlagolja az aktuális időt az időértékek esetleges kiugró értékeinek tudatlanságával, és “azt mondja az összes többi gépnek, hogy mozdítsák elő óráikat az új időre, vagy lassítsák le óráikat, amíg valamilyen meghatározott csökkentést nem érnek el” .

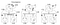
logikai órák

lépjünk vissza egy kicsit, és gondoljuk át újra a szinkronizált időbélyegek alapját. Az előző részben konkrét értékeket rendelünk a résztvevő gépek óráihoz, ezentúl megállapodhatnak egy globális ütemtervben, amelyen a rendszer végrehajtása során események történnek. Azonban, ami igazán számít az egész idővonalon, az a kapcsolódó események sorrendje. Például, ha valahogy csak kell tudni esemény történik, mielőtt esemény B, nem számít, ha Tₐ = 2, Tᵦ = 6 vagy Tₐ = 4, Tᵦ = 10, amíg Tₐ < Tᵦ. Ez a logikai órák birodalmára tereli figyelmünket, ahol a szinkronizálást Leslie Lamport “előtte történik” kapcsolat meghatározása befolyásolja .

Lamport logikai órái

fenomenális 1978-as papíridejében, óráiban és az események elosztott rendszerben történő rendezésében Lamport a következőképpen határozta meg a “happens-before” viszonyt”:

1. Ha a és b ugyanazon folyamat eseményei, és a B elé kerül, akkor a B.

2. Ha a egy üzenet elküldése egy folyamattal, b pedig ugyanazon üzenet fogadása egy másik folyamattal, akkor a B.

3. Ha a B és B C, akkor a C.

ha az X, y események különböző folyamatokban fordulnak elő, amelyek nem cserélnek üzeneteket, akkor sem x, sem y, sem y nem igaz, x és y egyidejű. Adott egy C függvény, amely C(a) időértéket rendel egy olyan eseményhez, amelyben minden folyamat megegyezik, ha a és b ugyanazon folyamat eseményei, és a B előtt fordul elő, C(a) < C(b)*. Hasonlóképpen, ha a Az üzenet küldése egy folyamat által, b pedig az üzenet fogadása egy másik folyamat által, C(a) < C (b)**.

most nézzük meg azt az algoritmust, amelyet Lamport javasolt az események időpontjainak hozzárendelésére. Tekintsük a következő példát egy klaszter 3 folyamatok A, B, C:

ezek a 3 folyamat órái a saját időzítésükön működnek, és kezdetben nincsenek szinkronban. Minden óra egy egyszerű szoftverszámlálóval valósítható meg, amelyet minden t időegység egy adott értékkel növekszik. Az óra növelésének értéke azonban folyamatonként eltérő: 1 A-Ra, 5 B-re és 2 C-re.

az 1. időpontban A M1 üzenetet küld B-nek. Mivel az üzenet elküldése időbélyegzővel történt az 1-es idővel, a B folyamat 10-es értéke minden bizonnyal lehetséges (arra következtethetünk, hogy 9 kullancsra volt szükség ahhoz, hogy B-be érkezzen A-ból).

most fontolja meg az M2 üzenetet. 15-kor hagyja el a B-t, és 8-kor érkezik a C-be. Ez az óra értéke C egyértelműen lehetetlen, mivel az idő nem megy hátra. * * – Tól és attól a ténytől, hogy az m2 15-kor indul, 16-ra vagy később kell megérkeznie. Ezért frissítenünk kell az aktuális időértéket C-nél, hogy nagyobb legyen, mint 15 (az egyszerűség kedvéért +1-et adunk az időhöz). Más szavakkal, amikor egy üzenet érkezik, és a vevő órája olyan értéket mutat, amely megelőzi az üzenet indulását jelző időbélyeget, a Vevő gyorsan előre továbbítja az óráját, hogy egy időegységgel több legyen, mint az indulási idő. A 6. ábrán azt látjuk, hogy az m2 most korrigálja az óra értékét C-nél 16-ra. Hasonlóképpen, az m3 és az m4 30, illetve 36-ra érkezik.

a fenti példából Maarten van Steen et al a következőképpen fogalmazza meg a Lamport algoritmusát:

1. Egy esemény végrehajtása előtt (azaz üzenet küldése a hálózaton keresztül, …), P! (P!) lépésekben C! (C!): C! (C!) < – C! (C!) + 1.

2. Amikor a P folyamat az M üzenetet küldi a Pj folyamathoz, az M időbélyegét állítja be ts(m) egyenlő C-vel az előző lépés végrehajtása után.

3. Az m üzenet kézhezvételekor a process Pj beállítja a saját helyi számlálóját Cj <- max{Cj, ts(m)} néven, majd végrehajtja az első lépést, és továbbítja az üzenetet az alkalmazásnak.

Vektorórák

Emlékezzünk vissza Lamport definíciójára A “történik-előtt” kapcsolatról, ha két olyan esemény van a és b között, hogy a B előtt következik be, akkor a is abban a sorrendben helyezkedik el b előtt, azaz C(a) < C(b). Ez azonban nem jelent fordított ok-okozati összefüggést, mivel nem következtethetünk arra, hogy a B elé kerül pusztán a C(a) és C(b) értékeinek összehasonlításával (a bizonyítás gyakorlatként marad az olvasó számára).

annak érdekében, hogy több információt nyerjünk az események időbélyeg alapján történő sorrendjéről, a Vector Clocks, a Lamport logikai órájának fejlettebb változata javasolt. A rendszer minden egyes P folyamatához az algoritmus vektort tart fenn VC ++ a következő attribútumokkal:

1. VC (VC): helyi logikai óra (p), vagy az aktuális időbélyeg előtt bekövetkezett események száma.

2. Ha VC = k, akkor P tudja, hogy K események történtek Pj – nél.

a Vektorórák algoritmusa ezután a következő:

1. Mielőtt futtatna egy esemény, Pᵢ feljegyzések egy új esemény történik, a saját maga által végrehajtó VCᵢ <- VCᵢ + 1.

2. Amikor a P (P) egy m (P) üzenetet küld Pj-nek, akkor az előző lépés végrehajtása után a TS(m) időbélyegzőt VC (C) – vel egyenlővé teszi.

3. Amikor az M üzenet érkezik, a folyamat pj frissíti a saját vektorórájának minden k-ját: vcj 6 max { vcj , ts(m)}. Ezután folytatja az első lépés végrehajtását, és továbbítja az üzenetet az alkalmazásnak.

ezekkel a lépésekkel, amikor egy folyamat Pj kap egy üzenetet m folyamat P ++ időbélyeggel ts(m), tudja, hogy az események száma, amelyek bekövetkeztek a P 6 véletlenül megelőzte a küldő m. továbbá, Pj is tud az eseményeket, amelyek már ismert, hogy P 0 más folyamatok elküldése előtt m. (Igen, ez igaz, ha a kapcsolódó algoritmus a pletyka protokollt, hogy ()).

remélhetőleg a magyarázat nem hagyja, hogy túl sokáig vakarja a fejét. Merüljünk bele egy példába a koncepció elsajátításához:

ebben a példában három folyamatunk van, a PNP, a P₂ és a PNP, amelyek alternatív módon üzeneteket cserélnek az órák szinkronizálására. A PNP az M1 üzenetet logikai időben küldi el a vcnp = (1, 0, 0) (1.lépés) a P₂-nak. P₂, miután megkapta az m1-et TS időbélyeggel(m1) = (1, 0, 0), a vc₂ logikai idejét (1, 1, 0) értékre állítja (3.lépés), és az M2 üzenetet időbélyeggel (1, 2, 0) (1. lépés) küldi vissza a PNP-nek. Hasonlóképpen, a PNP folyamat elfogadja az M2 üzenetet a P₂-tól, megváltoztatja logikai óráját (2, 2, 0) – re (3.lépés), majd az M3 üzenetet küldi a PNP-nek (3, 2, 0). A PNP az óráját (3, 2, 1) értékre állítja (1.lépés), miután megkapta az M3 üzenetet a PNP-től. Később felveszi az M4 üzenetet, amelyet a P₂ küldött (1, 4, 0), és ezáltal az óráját (3, 4, 2) értékre állítja (3.lépés).

annak alapján, hogy hogyan gyorsítjuk előre a szinkronizálás belső óráit, az a esemény megelőzi a b eseményt, ha minden k, ts(a) esetén van legalább egy K’ index, amelyre ts(a) < ts(b). Nem nehéz belátni, hogy (2, 2, 0) megelőzi (3, 2, 1), de (1, 4, 0) és (3, 2, 0) ütközhetnek egymással. Ezért vektorórákkal észlelhetjük, hogy van-e ok-okozati függőség bármely két esemény között.

elvenni

amikor a koncepció az idő elosztott rendszer, az elsődleges cél az, hogy elérjék a megfelelő sorrendben az események. Az események időrendi sorrendben helyezhetők el fizikai órákkal, vagy logikai sorrendben a Lamtport logikai óráival és Vektoróráival a végrehajtási idővonal mentén.

mi a következő lépés?

a sorozat következő részében áttekintjük, hogy az időszinkronizálás hogyan adhat meglepően egyszerű választ az elosztott rendszerek néhány klasszikus problémájára: legfeljebb egy üzenet , gyorsítótár-konzisztencia és kölcsönös kizárás .

Leslie Lamport: idő, órák és az események sorrendje elosztott rendszerben. 1978.

Barbara Liskov: a szinkronizált órák gyakorlati felhasználása elosztott rendszerekben. 1993.

Maarten van Steen, Andrew S. Tanenbaum: Elosztott Rendszerek. 2017.

Barbara Liskov, Liuba Shrira, John Wroclawski: Hatékony legfeljebb egyszer üzenetek szinkronizált órák alapján. 1991.

Cary G. Gray, David R. Cheriton: lízingek: hatékony hibatűrő mechanizmus az elosztott fájlok gyorsítótárának konzisztenciájához. 1989.

Ricardo Gusella, Stefano Zatti: a Tempo által elért Óraszinkronizálás pontossága a Berkeley UNIX 4.3 BSD-ben. 1989.