Konzisztens becslő: konzisztencia meghatározás & példák

statisztikai meghatározások > konzisztens becslő

mi az a konzisztens becslő?

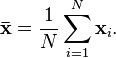
a minta átlaga a populáció átlagának következetes becslése.

a következetes becslés jelentéktelen hibákat (variációkat) tartalmaz, mivel a minta mérete nagyobb. Pontosabban, annak a valószínűsége, hogy ezek a hibák egy adott összegnél nagyobb mértékben változnak, a minta méretének növekedésével megközelíti a nullát. Más szavakkal, minél több adatot gyűjt, egy következetes becslő közel lesz a mérni kívánt valós populációs paraméterhez. A minta átlaga és a minta varianciája két jól ismert konzisztens becslés.

a konzisztencia gondolata alkalmazható a modellválasztásra is, ahol következetesen kiválasztja az “igaz” modellt a kapcsolódó “igaz” paraméterekkel. Például a illeszkedési teszt jósága a konzisztencia mértékeként is használható. Az illesztési teszt egyik népszerű jósága a chi-négyzet teszt, amely azon a feltevésen alapul, hogy az adatok várható értékei megfelelnek a normál eloszlásnak. Ha pedig idősoros modellből származó adatokkal rendelkezik, akkor az adatok konzisztenciája mérhető egy autoregresszív modellel. Számos más következetességi intézkedés létezik az adatoknak a modellekhez való illesztéséhez. Az, hogy melyik módszert használja, attól függ, hogy mit szeretne mérni az adatai. Például, úgy gondolja, hogy adatai lineáris tendenciát követnek, exponenciális trend, vagy egy olyan konkrét trend, mint amilyet ebben a cikkben látunk, amely a pénzügyi modellek zavarkomponenseinek következetes becslését vázolja fel?

eredet

a konzisztens becslő kifejezés a “becslők következetes sorrendje” rövidítése, amely a valószínűség konvergenciájában található ötlet. Az alapötlet az, hogy ismételje meg a becslő eredményeit újra és újra, folyamatosan növekvő mintaméretekkel. Végül-feltételezve — hogy a becslője következetes — a szekvencia konvergál a valódi populációs paraméteren. Ezt a konvergenciát határnak nevezzük, amely a számítás alapvető építőköve.

Cram Ons, H. (1946). A statisztika matematikai módszerei”, Princeton Univ. Nyomja Meg Az I. A. Ibragimov, R. Z. Has ‘ minskii, (1981)” statisztikai becslés: aszimptotikus elmélet”, Springer. (Oroszul lefordítva)
Levinsohn, J. & MacKie-Mason, J. (1989). Egy egyszerű, hátrányok. est. a pénzügyi modellek zavarkomponenseihez. Nemzeti Gazdaságkutató Iroda. MŰSZAKI munkadokumentum 80. Lap január 7, 2017 származó http://www.nber.org/papers/t0080.pdf.

——————————————————————————

segítségre van szüksége a házi feladat vagy teszt kérdés? A Chegg Study segítségével lépésről lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!