teljes metrikus tér

a matematikában a teljes metrikus tér olyan metrikus tér, amelyben minden Cauchy-szekvencia konvergens. Más szavakkal, a metrikus térben minden Cauchy-szekvencia a határon egy olyan pontra hajlik, amely ismét ennek a térnek az eleme. Ezért a metrikus tér bizonyos értelemben ” teljes.”

• 1 formális meghatározás
• 2 példa
• 3 Befejezés
  • 3.1 példák
• 4 topológiailag teljes tér
• 5 Lásd még

formális definíció

legyen X metrikus tér metrikus d. akkor X teljes, ha minden Cauchy-szekvenciához 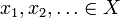van egy 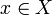elem, amely .

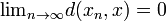példák

• a valós számok R, és általánosabban véges dimenziós euklideszi terek, a szokásos metrikus teljesek.
• bármely kompakt metrikus tér egymás után kompakt, ezért teljes. A fordított nem érvényes: például R teljes, de nem kompakt.
• a diszkrét metrikával rendelkező térben az egyetlen Cauchy-szekvencia azok, amelyek egy bizonyos ponttól állandóak. Ezért minden diszkrét metrikus tér teljes. Így néhány korlátozott teljes metrikus tér nem kompakt.
• a Q racionális számok nem teljesek. Például az x0 = 1, xn+1 = 1 + 1/xn által meghatározott szekvencia Cauchy, de nem konvergál Q-ban.)

Befejezés

minden X metrikus térnek van befejezése 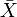amely egy teljes metrikus tér, amelyben X izometrikusan sűrű altérként van beágyazva. A befejezésnek univerzális tulajdonsága van.

példák

• az R valós számok a racionális számok befejezése Q az abszolút távolság szokásos metrikájához viszonyítva.

topológiailag teljes tér

a teljesség nem topológiai tulajdonság: lehetséges, hogy egy teljes metrikus tér homeomorf legyen egy nem teljes metrikus térrel. Például az R valós vonal homeomorf egy nyitott intervallummal, mondjuk (0,1). Egy másik példa: a

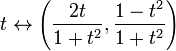
térkép egy homeomorfizmus a teljes metrikus tér között R és a hiányos tér,amely az Egységkör az euklideszi síkban a (0, -1) ponttal törölve. Ez utóbbi tér nem teljes, mivel a nem Cauchy-szekvencia megfelel t=n mint n végigfut a pozitív egész számokon, a kör nem konvergens Cauchy-szekvenciájára van leképezve.

meghatározhatunk egy topológiai teret metrikusan topológiailag teljesnek, ha homeomorf a teljes metrikus tér. Ennek a tulajdonságnak a topológiai feltétele az, hogy a tér metrizálható legyen, és abszolút g legyen (g) minden topológiai térben, amelybe beágyazható (vagy csak g)). Különösen az euklideszi terek összes nyitott részhalmaza metrikusan topológiailag teljes.

Lásd még:

• Banach-tér
• Hilbert-tér

előfordulhat, hogy ezen az oldalon néhány tartalom korábban megjelent a Citizendium oldalon.