Addizione vettoriale

Quando abbiamo menzionato nell’introduzione che un vettore è una coppia ordinata o una tripletta di numeri, abbiamo implicitamente definito i vettori in termini di componenti.

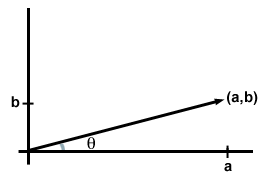
Ogni voce nella coppia ordinata 2-dimensionale (a, b) o tripletta 3-dimensionale (a, b, c) è chiamata componente del vettore. Se non diversamente specificato, normalmente si intende che le voci corrispondono al numero di unità che il vettore ha nelle direzioni x, y e (per il caso 3D) z di un piano o di uno spazio. In altre parole, puoi pensare ai componenti semplicemente come alle coordinate del punto associato al vettore. (In un certo senso, il vettore è il punto, anche se quando disegniamo vettori normalmente disegniamo una freccia dall’origine al punto.)

Aggiunta vettoriale utilizzando componenti

Dati due vettori u = (u1, u2) e v = (v1, v2) nel piano euclideo, la somma è data da:

Per tre-dimensionale vettori u = (u1, u2, u3) e v = (v1, v2, v3), la formula è quasi identico:

In altre parole, la somma vettoriale è proprio come l’ordinaria inoltre: componente per componente.

Si noti che se si sommano due vettori 2-dimensionali è necessario ottenere un altro vettore 2-dimensionale come risposta. L’aggiunta di vettori 3-dimensionali produrrà risposte 3-dimensionali. i vettori a 2 e 3 dimensioni appartengono a spazi vettoriali diversi e non possono essere aggiunti. Queste stesse regole si applicano quando abbiamo a che fare con la moltiplicazione scalare.