Completo di spazio metrico

In matematica, un completo spazio metrico è uno spazio metrico in cui ogni successione di Cauchy è convergente. In altre parole, ogni sequenza di Cauchy nello spazio metrico tende nel limite a un punto che è di nuovo un elemento di quello spazio. Quindi lo spazio metrico è, in un certo senso, “completo.”

• 1 definizione Formale
• 2 Esempi
• 3 Completamento
  • 3.1 Esempi
• 4 Topologicamente completare lo spazio
• 5

Definizione formale

sia X uno spazio metrico con la metrica d. Allora X è completo se ogni successione di Cauchy 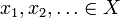c’è un elemento 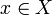tali che .

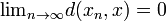Esempi

• I numeri reali R, e più in generale gli spazi Euclidei a dimensione finita, con la metrica usuale sono completi.
• Qualsiasi spazio metrico compatto è sequenzialmente compatto e quindi completo. Il contrario non regge: ad esempio, R è completo ma non compatto.
• In uno spazio con la metrica discreta, le uniche sequenze di Cauchy sono quelle che sono costanti da un certo punto in poi. Quindi qualsiasi spazio metrico discreto è completo. Pertanto, alcuni spazi metrici completi delimitati non sono compatti.
• I numeri razionali Q non sono completi. Ad esempio, la sequenza (xn) definita da x0 = 1, xn+1 = 1 + 1/xn è Cauchy, ma non converge in Q. (In R converge in un numero irrazionale.)

Completamento

Ogni spazio metrico X ha un completamento 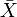che è uno spazio metrico completo in cui X è incorporato isometricamente come un sottospazio denso. Il completamento ha una proprietà universale.

Esempi

• I numeri reali R sono il completamento dei numeri razionali Q rispetto alla metrica usuale della distanza assoluta.

Spazio topologicamente completo

La completezza non è una proprietà topologica: è possibile che uno spazio metrico completo sia omeomorfo a uno spazio metrico non completo. Ad esempio, la linea reale R è omeomorfa a un intervallo aperto, ad esempio, (0,1). Un altro esempio: la mappa

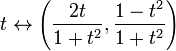
è un omeomorfismo tra lo spazio metrico completo R e lo spazio incompleto che è il cerchio unitario nel piano Euclideo con il punto (0,-1) cancellato. Quest’ultimo spazio non è completo poiché la sequenza non-Cauchy corrispondente a t=n mentre n attraversa gli interi positivi è mappata su una sequenza di Cauchy non convergente sul cerchio.

Possiamo definire uno spazio topologico per essere metricalmente topologicamente completo se è omeomorfo a uno spazio metrico completo. Una condizione topologica per questa proprietà è che lo spazio sia metrizzabile e un Gδ assoluto, cioè un Gδ in ogni spazio topologico in cui può essere incorporato (o solo Gδ nel suo completamento in una metrica scelta). In particolare, tutti i sottoinsiemi aperti degli spazi euclidei sono metricamente topologicamente completi.

Vedi anche

• Spazio di Banach
• Spazio di Hilbert

Alcuni contenuti di questa pagina potrebbero essere già apparsi su Citizendium.