Concavo Scafo

la Creazione di un cluster di bordo utilizzando un K-nearest neighbors approccio

Un paio di mesi fa, Ho scritto qui su Media un articolo sulla mappatura del regno UNITO incidenti stradali hot spot. Ero principalmente preoccupato di illustrare l’uso dell’algoritmo di clustering DBSCAN sui dati geografici. Nell’articolo, ho usato informazioni geografiche pubblicate dal governo del Regno Unito sugli incidenti stradali segnalati. Il mio scopo era quello di eseguire un processo di clustering basato sulla densità per trovare le aree in cui gli incidenti stradali sono segnalati più frequentemente. Il risultato finale è stata la creazione di una serie di geo-recinzioni che rappresentano questi punti caldi di incidente.

Raccogliendo tutti i punti in un determinato cluster, puoi avere un’idea di come sarebbe il cluster su una mappa, ma ti mancherà un’importante informazione: la forma esterna del cluster. In questo caso, stiamo parlando di un poligono chiuso che può essere rappresentato su una mappa come un geo-recinto. Si può presumere che qualsiasi punto all’interno del geo-fence appartenga al cluster, il che rende questa forma un’interessante informazione: puoi usarla come funzione discriminatrice. Si può presumere che tutti i punti appena campionati che rientrano nel poligono appartengano al cluster corrispondente. Come ho accennato nell’articolo, è possibile utilizzare tali poligoni per affermare il rischio di guida, utilizzandoli per classificare la propria posizione GPS campionata.

La domanda ora è come creare un poligono significativo da una nuvola di punti che compongono un cluster specifico. Il mio approccio nel primo articolo era un po ‘ ingenuo e rifletteva una soluzione che avevo già usato nel codice di produzione. Questa soluzione comportava il posizionamento di un cerchio centrato in ciascuno dei punti del cluster e quindi la fusione di tutti i cerchi per formare un poligono a forma di nuvola. Il risultato non è molto bello, né realistico. Inoltre, utilizzando i cerchi come forma di base per la costruzione del poligono finale, questi avranno più punti di una forma più snella, aumentando così i costi di archiviazione e rendendo gli algoritmi di rilevamento dell’inclusione più lenti da eseguire.

d’altra parte, questo approccio ha il vantaggio di essere computazionalmente semplice (almeno dalla vista dello sviluppatore), in quanto utilizza Formosa s cascaded_union funzione di unire tutti i cerchi insieme. Un altro vantaggio è che la forma del poligono viene definita implicitamente utilizzando tutti i punti del cluster.

Per approcci più sofisticati, dobbiamo in qualche modo identificare i punti di confine del cluster, quelli che sembrano definire la forma della nuvola di punti. È interessante notare che con alcune implementazioni DBSCAN è possibile recuperare i punti di confine come sottoprodotto del processo di clustering. Sfortunatamente, questa informazione non è (apparentemente) disponibile sull’implementazione di SciKit Learn, quindi dobbiamo accontentarci.

Il primo approccio che mi è venuto in mente è stato quello di calcolare lo scafo convesso dell’insieme di punti. Questo è un ben compreso algoritmo, ma soffre il problema di non manipolazione di forme concave, come questo:

Questa forma non correttamente catturare l’essenza del sottostante punti. Se fosse usato come discriminatore, alcuni punti sarebbero erroneamente classificati come all’interno del cluster quando non lo sono. Abbiamo bisogno di un altro approccio.

L’alternativa dello scafo concavo

Fortunatamente, ci sono alternative a questo stato di cose: possiamo calcolare uno scafo concavo. Ecco come appare lo scafo concavo quando applicato allo stesso insieme di punti dell’immagine precedente:

O forse questo:

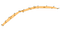
Come puoi vedere, e contrariamente allo scafo convesso, non esiste un’unica definizione di cosa sia lo scafo concavo di un insieme di punti. Con l’algoritmo che sto presentando qui, la scelta di quanto concavo vuoi che siano i tuoi scafi è fatta attraverso un singolo parametro: k — il numero di vicini più vicini considerati durante il calcolo dello scafo. Vediamo come funziona.

L’algoritmo

L’algoritmo che presento qui è stato descritto oltre un decennio fa da Adriano Moreira e Maribel Yasmina Santos dell’Università di Minho, in Portogallo . Dall’abstract:

Questo documento descrive un algoritmo per calcolare l’inviluppo di un insieme di punti in un piano, che genera convesso su scafi non convessi che rappresentano l’area occupata dai punti dati. L’algoritmo proposto si basa su un approccio k-nearest neighbors, in cui il valore di k, l’unico parametro dell’algoritmo, viene utilizzato per controllare la “scorrevolezza” della soluzione finale.

Poiché applicherò questo algoritmo alle informazioni geografiche, è stato necessario apportare alcune modifiche, vale a dire quando si calcolano angoli e distanze . Ma questi non alterano in alcun modo l’essenza dell’algoritmo, che può essere ampiamente descritto dai seguenti passaggi:

1. Trova il punto con la coordinata y (latitudine) più bassa e rendilo quello corrente.
2. Trova i punti k-più vicini al punto corrente.
3. Dai punti k-più vicini, selezionare quello che corrisponde al giro più grande a destra dall’angolo precedente. Qui useremo il concetto di cuscinetto e inizieremo con un angolo di 270 gradi (verso ovest).
4. Controlla se aggiungendo il nuovo punto alla stringa di linea crescente, non si interseca da solo. In tal caso, selezionare un altro punto dal k-più vicino o riavviare con un valore maggiore di k.
5. Rendere il nuovo punto il punto corrente e rimuoverlo dall’elenco.
6. Dopo k iterazioni aggiungere il primo punto di nuovo alla lista.
7. Ciclo al numero 2.

L’algoritmo sembra essere abbastanza semplice, ma ci sono una serie di dettagli che devono essere curati, soprattutto perché abbiamo a che fare con le coordinate geografiche. Distanze e angoli sono misurati in un modo diverso.

Il codice

Qui sto pubblicando è una versione adattata del codice dell’articolo precedente. Troverai comunque lo stesso codice di clustering e lo stesso generatore di cluster a forma di nuvola. La versione aggiornata ora contiene un pacchetto denominato geomath.hulls in cui è possibile trovare la classe ConcaveHull. Per creare i tuoi scafi concavi fai come segue:

Nel codice sopra, points è una matrice di dimensioni (N, 2), in cui le righe contengono i punti osservati e le colonne contengono le coordinate geografiche (longitudine, latitudine). L’array risultante ha esattamente la stessa struttura, ma contiene solo i punti che appartengono alla forma poligonale del cluster. Un filtro di sorta.

Poiché gestiremo gli array è naturale portare NumPy nella mischia. Tutti i calcoli sono stati debitamente vettorializzati, quando possibile, e sono stati fatti sforzi per migliorare le prestazioni durante l’aggiunta e la rimozione di elementi dagli array (spoiler: non vengono spostati affatto). Uno dei miglioramenti mancanti è la parallelizzazione del codice. Ma questo può aspettare.

Ho organizzato il codice attorno all’algoritmo come esposto nel documento, anche se alcune ottimizzazioni sono state fatte durante la traduzione. L’algoritmo è costruito attorno a una serie di subroutine che sono chiaramente identificate dal documento, quindi togliamole di mezzo adesso. Per la vostra comodità di lettura, userò gli stessi nomi usati nel giornale.

CleanList-La pulizia dell’elenco dei punti viene eseguita nel costruttore della classe:

Come puoi vedere, l’elenco dei punti è implementato come un array NumPy per motivi di prestazioni. La pulizia dell’elenco viene eseguita sulla linea 10, dove vengono mantenuti solo i punti unici. L’array di set di dati è organizzato con osservazioni in righe e coordinate geografiche nelle due colonne. Si noti che sto anche creando un array booleano sulla riga 13 che verrà utilizzato per indicizzare l’array principale del set di dati, facilitando il lavoro di rimozione degli elementi e, una volta ogni tanto, aggiungendoli di nuovo. Ho visto questa tecnica chiamata “maschera” sulla documentazione NumPy, ed è molto potente. Per quanto riguarda i numeri primi, li discuterò più tardi.

FindMinYPoint-Questo richiede una piccola funzione:

Questa funzione viene chiamata con l’array dataset come argomento e restituisce l’indice del punto con la latitudine più bassa. Si noti che le righe sono codificate con longitudine nella prima colonna e latitudine nella seconda.

RemovePoint
AddPoint — Questi sono no-brainers, a causa dell’uso dell’array indices. Questo array viene utilizzato per memorizzare gli indici attivi nell’array principale del set di dati, quindi rimuovere gli elementi dal set di dati è un gioco da ragazzi.

Sebbene l’algoritmo descritto nel documento richieda l’aggiunta di un punto all’array che costituisce lo scafo, questo viene effettivamente implementato come:

Successivamente, la variabile test_hull verrà assegnata a hull quando la stringa di linea viene considerata non intersecante. Ma sto andando avanti del gioco qui. La rimozione di un punto dall’array dataset è semplice come:

self.indices = False

Aggiungerlo è solo una questione di capovolgere quel valore dell’array allo stesso indice fino a true. Ma tutta questa convenienza viene fornito con il prezzo di dover tenere sotto controllo gli indici. Più su questo più tardi.

NearestPoints-Le cose iniziano a diventare interessanti qui perché non abbiamo a che fare con coordinate planari, quindi fuori con Pitagora e dentro con Haversine:

Si noti che il secondo e il terzo parametro sono array nel formato del set di dati: longitudine nella prima colonna e latitudine nella seconda. Come puoi vedere, questa funzione restituisce una matrice di distanze in metri tra il punto nel secondo argomento e i punti nel terzo argomento. Una volta che abbiamo questi, possiamo ottenere il k-vicini più vicini il modo più semplice. Ma c’è una funzione specializzata per questo e merita alcune spiegazioni:

La funzione inizia creando un array con gli indici di base. Questi sono gli indici dei punti che non sono stati rimossi dall’array di set di dati. Ad esempio, se su un cluster di dieci punti abbiamo iniziato rimuovendo il primo punto, l’array di indici di base sarebbe . Successivamente, calcoliamo le distanze e ordiniamo gli indici di array risultanti. I primi k vengono estratti e quindi utilizzati come maschera per recuperare gli indici di base. È un po ‘ contorto ma funziona. Come puoi vedere, la funzione non restituisce un array di coordinate, ma un array di indici nell’array del set di dati.

SortByAngle – Ci sono più problemi qui perché non stiamo calcolando angoli semplici, stiamo calcolando i cuscinetti. Questi sono misurati come zero gradi verso nord, con angoli crescenti in senso orario. Ecco il nucleo del codice che calcola i cuscinetti:

La funzione restituisce una serie di cuscinetti misurati dal punto il cui indice si trova nel primo argomento, ai punti i cui indici si trovano nel terzo argomento. L’ordinamento è semplice:

A questo punto, l’array candidati contiene gli indici dei punti k-più vicini ordinati per ordine decrescente di cuscinetto.

IntersectQ-Invece di rotolare le mie funzioni di intersezione di linea, mi sono rivolto a Shapely per chiedere aiuto. Infatti, mentre costruiamo il poligono, stiamo essenzialmente gestendo una stringa di linea, aggiungendo segmenti che non si intersecano con quelli precedenti. Il test per questo è semplice: raccogliamo l’array di hull in costruzione, lo convertiamo in un oggetto string line formoso e verifichiamo se è semplice (non auto-intersecante) o meno.

In poche parole, una stringa di linea formosa diventa complessa se si auto-attraversa, quindi il predicato is_simple diventa falso. Easy.

PointInPolygon-Questo si è rivelato essere il più complicato da implementare. Permettetemi di spiegare guardando il codice che esegue la convalida finale del poligono dello scafo (controlla se tutti i punti del cluster sono inclusi nel poligono):

Le funzioni di Shapely per testare l’intersezione e l’inclusione dovrebbero essere state sufficienti per verificare se il poligono finale dello scafo si sovrappone a tutti i punti del cluster, ma non lo erano. Perché? Shapely è indipendente dalle coordinate, quindi gestirà le coordinate geografiche espresse in latitudini e longitudini esattamente allo stesso modo delle coordinate su un piano cartesiano. Ma il mondo si comporta in modo diverso quando si vive su una sfera, e gli angoli (o cuscinetti) non sono costanti lungo una geodetica. L’esempio di riferimento di una linea geodetica che collega Baghdad a Osaka lo illustra perfettamente. Accade così che in alcune circostanze, l’algoritmo può includere un punto basato sul criterio del cuscinetto, ma in seguito, usando gli algoritmi planari di Shapely, essere considerato sempre leggermente al di fuori del poligono. Questo è ciò che la piccola correzione della distanza sta facendo lì.

Mi ci è voluto un po ‘ per capirlo. Il mio aiuto per il debug è stato QGIS, un grande pezzo di software libero. Ad ogni passo dei calcoli sospetti, inviavo i dati in formato WKT in un file CSV da leggere come livello. Un vero salvagente!

Infine, se il poligono non riesce a coprire tutti i punti del cluster, l’unica opzione è aumentare k e riprovare. Qui ho aggiunto un po ‘ della mia intuizione.

Prime k

L’articolo suggerisce che il valore di k sia aumentato di uno e che l’algoritmo venga eseguito nuovamente da zero. I miei primi test con questa opzione non erano molto soddisfacenti: i tempi di esecuzione sarebbero stati lenti su cluster problematici. Ciò era dovuto al lento aumento di k, quindi ho deciso di utilizzare un altro programma di aumento: una tabella di numeri primi. L’algoritmo inizia già con k=3, quindi è stata un’estensione facile per farlo evolvere su un elenco di numeri primi. Questo è ciò che vedi accadere nella chiamata ricorsiva:

Ho una cosa per i numeri primi, sai

Blow Up

I poligoni dello scafo concavo generati da questo algoritmo hanno ancora bisogno di ulteriori elaborazioni, perché discrimineranno solo i punti all’interno dello scafo, ma non vicino ad esso. La soluzione è aggiungere un po ‘ di imbottitura a questi cluster magri. Qui sto usando la stessa tecnica usata prima, ed ecco come appare:

Qui, ho usato la funzione buffer di Shapely per fare il trucco.

La funzione accetta un poligono sagomato e restituisce una versione gonfiata di se stessa. Il secondo parametro è il raggio in metri del padding aggiunto.

Esecuzione del codice

Inizia estraendo il codice dal repository GitHub nella tua macchina locale. Il file che si desidera eseguire è ShowHotSpots.py nella directory principale. Alla prima esecuzione, il codice leggerà nel Regno Unito i dati sugli incidenti stradali dal 2013 al 2016 e lo raggrupperà. I risultati vengono quindi memorizzati nella cache come file CSV per le esecuzioni successive.

Ti verranno quindi presentate due mappe: la prima viene generata utilizzando i cluster a forma di nuvola mentre la seconda utilizza l’algoritmo di clustering concavo discusso qui. Mentre il codice di generazione del poligono viene eseguito, è possibile che vengano segnalati alcuni errori. Per aiutare a capire perché l’algoritmo non riesce a creare uno scafo concavo, il codice scrive i cluster in file CSV nella directory data/out/failed/. Come al solito, è possibile utilizzare QGIS per importare questi file come livelli.

Essenzialmente questo algoritmo fallisce quando non trova abbastanza punti per “aggirare” la forma senza auto-intersecarsi. Ciò significa che devi essere pronto a scartare questi cluster o ad applicare un trattamento diverso a loro (scafo convesso o bolle coalizzate).

Concavità

È un involucro. In questo articolo ho presentato un metodo di post-elaborazione DBSCAN generato cluster geografici in forme concave. Questo metodo può fornire un poligono esterno più adatto per i cluster rispetto ad altre alternative.

Grazie per la lettura e godere armeggiare con il codice!

Kryszkiewicz M., Lasek P. (2010) TI-DBSCAN: Clustering con DBSCAN per mezzo della disuguaglianza triangolare. In: Szczuka M., Kryszkiewicz M., Ramanna S., Jensen R., Hu Q. (eds) Rough Sets and Current Trends in Computing. RSCTC 2010. Lecture Notes in Computer Science, vol 6086. Springer, Berlin, Heidelberg

Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pagg. 2825-2830, 2011

Moreira, A. and Santos, M. Y., 2007, Concave Hull: A K-nearest neighbors approach for the computation of the region occupied by a set of points

Calcola la distanza, il cuscinetto e altro tra i punti di latitudine/Longitudine

GitHub repository