Punti di vita di Cogs

by Posted on

Cogs hanno un certo numero di punti di vita (HP) a seconda del loro livello. Gli ingranaggi di livello 1 hanno la più bassa quantità di HP, mentre gli ingranaggi di livello 12 hanno la più alta quantità di HP.

La tabella seguente mostra quanti HP ha ogni livello Cog e quali gag possono sconfiggere il Cog in un colpo. Alcune gag potrebbero dover essere organiche.

Livello punti One-hit gag
1 6 Cupcake (6 danni)
Vaso di Fiori (10 danni)
Bicchiere d’Acqua (6 danni)
2 12 Buccia di Banana (12 danni)
Pistola a Spruzzo (12 danni)
sacchetto di sabbia (18 danni)
3 20 Rake (20 danni)
Proboscide di Elefante (21 danni)
Seltz Bottiglia (21 danni)
4 30 Manichetta Antincendio (30 danni)
Incudine (30 danni)
Marmi (35 danni)
5 42 Grande Peso (45 danni)
Organico Tutta la Torta di Panna (44 danni)
sabbie mobili (50 danni)
6 56 cassetta di Sicurezza (a 60 danni)
Botola (70 danni)
7 72 Organico Botola (77 danni)
Nube di Tempesta (80 danni)
8 90 Cantante Lirica (90 danni)
Torta di Compleanno (100 danni)
9 110 Organico Torta di Compleanno (110 danni)
Organica Geyser (115 danni)
10 132 Organico Torta di Nozze (132 danni)
11 156 Pianoforte a coda (170 danni)
TNT (180 danni)
12 200 Organico Ferrovia (214 danni)

Formule

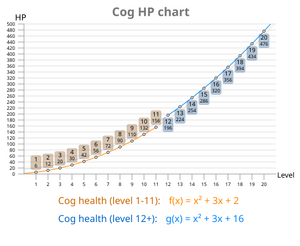
Un grafico che mostra la salute, la crescita dei Denti dal loro livello. La differenza di salute degli ingranaggi di livello 12 può essere vista.

La formula per la salute di un ingranaggio può essere:

{\displaystyle f (x)=x^{2} + 3x + 2}

o in modo semplificato:

{\displaystyle f (x)=(x+1)\times (x+2)}

dove x è il livello dell’ingranaggio e f (x) è una funzione che restituisce il valore di salute degli ingranaggi.

Per esempio, la formula funziona nel seguente metodo per il livello quattro Denti, che hanno 30 HP:

{\displaystyle f(4)=(4+1)\volte (4+2)} {\displaystyle f(4)=(5)\times (6)} {\displaystyle f(4)=30}

La formula precedente si applica a tutti i Cog livello, se non a livello 12, che ha 200 CV.

per recuperare i Cog livello da un dato HP, piuttosto che il recupero di HP dal livello, formula quadratica può essere utilizzato dove n è il HP:

{\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9-4*(2-n)}}}{2}}}

Per esempio, l’equazione sarà risolto nel seguente metodo per capire quale Cog avrebbe 156 CV:

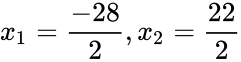
{\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9-4*(2-156)}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9-4*-154}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9+616}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {625}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm 25}{2}}} {\displaystyle x_{1}={\frac {-3-25}{2}},x_{2}={\frac {-3+25}{2}}} {\displaystyle x_{1}={\frac {-28}{2}},x_{2}={\frac {22}{2}}} {\displaystyle x_{1}=-14,x_{2}=11}

Dal momento che f(x) è una funzione di una parabola e nessuna delle soluzioni è il valore minimo della funzione, ci sono due risposte per l’equazione: -14, che non è un livello di Cog reale; e 11, che è un livello reale.

Sebbene questa formula funzioni per tutti i livelli di Cog, quando si va oltre i normali livelli di Cog, questa formula inizia ad essere inapplicabile nella pratica a causa di numeri complessi. Per qualsiasi valore n inferiore a -0,25, questa equazione introduce numeri complessi, che funzionano ancora in teoria ma non in pratica.

Curiosità

  • Anche se gli ingranaggi di livello 12 dovrebbero avere 182 CV, hanno invece 200, che è essenzialmente un aumento del 10%. Secondo la formula, un ingranaggio con 200 CV dovrebbe essere di circa il livello 12.65 (o circa -15.65, anche se i valori negativi non sono compatibili con i livelli di ingranaggio).
  • Secondo la formula, il direttore di Ambush Marketing avrebbe 2.652 HP, dato che è di livello 50.

Published by admin

Lascia un commento

Il tuo indirizzo email non sarà pubblicato.