Tempo di Sincronizzazione nei Sistemi Distribuiti

Se ti trovi familiarità con siti web come facebook.com o google.com, forse non meno di una volta vi siete chiesti come questi siti web in grado di gestire milioni o addirittura decine di milioni di richieste al secondo. Ci sarà un singolo server commerciale in grado di sopportare questa enorme quantità di richieste, nel modo in cui ogni richiesta può essere servita tempestivamente per gli utenti finali?

Immergendosi più in profondità in questa materia, arriviamo al concetto di sistemi distribuiti, una raccolta di computer indipendenti (o nodi) che appaiono ai suoi utenti come un unico sistema coerente. Questa nozione di coerenza per gli utenti è chiara, poiché credono di avere a che fare con una singola macchina gigantesca che assume la forma di più processi in esecuzione in parallelo per gestire batch di richieste contemporaneamente. Tuttavia, per le persone che capiscono l’infrastruttura del sistema, le cose non risultano così facili come tali.

Per migliaia di macchine indipendenti in esecuzione contemporaneamente che possono estendersi su più fusi orari e continenti, è necessario fornire alcuni tipi di sincronizzazione o coordinamento per consentire a queste macchine di collaborare in modo efficiente tra loro (in modo che possano apparire come uno). In questo blog, discuteremo la sincronizzazione del tempo e come raggiunge la coerenza tra le macchine su ordinazione e causalità degli eventi.

Il contenuto di questo blog sarà organizzato come segue:

1. Sincronizzazione dell’orologio
2. Orologi logici
3. Take away
4. Quali sono le prospettive?

Orologi fisici

In un sistema centralizzato, il tempo non è ambiguo. Quasi tutti i computer hanno un “orologio in tempo reale” per tenere traccia del tempo, di solito in sincronia con un cristallo di quarzo lavorato con precisione. Sulla base dell’oscillazione di frequenza ben definita di questo quarzo, il sistema operativo di un computer può monitorare con precisione il tempo interno. Anche quando il computer è spento o si esaurisce, il quarzo continua a spuntare a causa della batteria CMOS, una piccola centrale elettrica integrata nella scheda madre. Quando il computer si connette alla rete (Internet), il sistema operativo contatta un server timer, dotato di un ricevitore UTC o di un orologio preciso, per ripristinare con precisione il timer locale utilizzando il Network Time Protocol, chiamato anche NTP.

Sebbene questa frequenza del quarzo cristallino sia ragionevolmente stabile, è impossibile garantire che tutti i cristalli di computer diversi funzionino esattamente alla stessa frequenza. Immaginate un sistema con n computer, il cui ogni cristallo in esecuzione a velocità leggermente diverse, causando gli orologi a poco a poco per uscire di sincronizzazione e dare valori diversi quando lettura. La differenza nei valori di tempo causati da questo è chiamata inclinazione dell’orologio.

In questa circostanza, le cose si sono incasinate per avere più macchine separate spazialmente. Se l’uso di più orologi fisici interni è auspicabile, come li sincronizziamo con gli orologi del mondo reale? Come li sincronizziamo l’uno con l’altro?

Network Time Protocol

Un approccio comune per la sincronizzazione a coppie tra computer è attraverso l’uso del modello client-server, ovvero lasciare che i client contattino un time server. Consideriamo il seguente esempio con 2 macchine A e B:

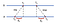
In primo luogo, A invia una richiesta timestamped con valore t to a B. B, all’arrivo del messaggio, registra l’ora di ricezione T₁ dal proprio orologio locale e le risposte con un messaggio timestamped con T₂, piggybacking il valore precedentemente registrato t₁. Infine, A, dopo aver ricevuto la risposta da B, registra l’orario di arrivo T₃. Per tenere conto del ritardo nella consegna dei messaggi, calcoliamo δ₁ = t T-t₀, Δ₂ = T T-T₂. Ora, un offset stimato di A rispetto a B è:

Basato su θ, possiamo rallentare l’orologio di A o fissarlo in modo che le due macchine possano essere sincronizzate tra loro.

Poiché NTP è applicabile a coppie, l’orologio di B può essere regolato anche su quello di A. Tuttavia, non è saggio regolare l’orologio in B se è noto per essere più accurato. Per risolvere questo problema, NTP divide i server in strati, cioè classifica i server in modo che gli orologi da server meno precisi con ranghi più piccoli saranno sincronizzati con quelli di quelli più precisi con ranghi più alti.

Algoritmo di Berkeley

In contrasto con i client che contattano periodicamente un time server per la sincronizzazione dell’ora esatta, Gusella e Zatti, nel 1989 Berkeley Unix paper , proposero il modello client-server in cui il time server (daemon) esegue periodicamente sondaggi su ogni macchina per chiedere a che ora è lì. Sulla base delle risposte, calcola il tempo di andata e ritorno dei messaggi, calcola in media l’ora corrente con l’ignoranza di eventuali valori anomali nei valori temporali e “dice a tutte le altre macchine di far avanzare i loro orologi al nuovo tempo o rallentare i loro orologi fino a quando non è stata raggiunta una riduzione specificata” .

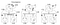
Orologi logici

Facciamo un passo indietro e riconsideriamo la nostra base per i timestamp sincronizzati. Nella sezione precedente, assegniamo valori concreti agli orologi di tutte le macchine partecipanti, d’ora in poi possono concordare una timeline globale in cui gli eventi accadono durante l’esecuzione del sistema. Tuttavia, ciò che conta davvero in tutta la timeline è l’ordine in cui si verificano eventi correlati. Per esempio, se in qualche modo abbiamo solo bisogno di sapere Un evento accade prima di un evento B, non importa se Tₐ = 2, Tᵦ = 6 o Tₐ = 4, Tᵦ = 10, purché Tₐ < Tᵦ. Questo sposta la nostra attenzione sul regno degli orologi logici, dove la sincronizzazione è influenzata dalla definizione di Leslie Lamport di relazione “accade-prima”.

Lamport’s Logical Clocks

Nel suo fenomenale paper del 1978 Time, Clocks, and the Ordering of Events in a Distributed System , Lamport definì la relazione “happens-before” → ” come segue:

1. Se a e b sono eventi nello stesso processo e a viene prima di b, allora a→b.

2. Se a è l’invio di un messaggio da parte di un processo e b è la ricezione dello stesso messaggio da parte di un altro processo, allora a→b.

3. Se a→b e b→c, allora a→c.

Se gli eventi x, y si verificano in processi diversi che non scambiano messaggi, né x → y né y → x è vero, x e y sono considerati simultanei. Data una funzione C che assegna un valore temporale C (a) per un evento su cui tutti i processi concordano, se a e b sono eventi all’interno dello stesso processo e a si verifica prima di b, C(a) < C(b)*. Allo stesso modo, se a è l’invio di un messaggio da parte di un processo e b è la ricezione di quel messaggio da parte di un altro processo, C(a) < C(b) **.

Ora diamo un’occhiata all’algoritmo che Lamport ha proposto per assegnare i tempi agli eventi. Consideriamo il seguente esempio con un cluster di 3 processi A, B, C:

Gli orologi di questi 3 processi funzionano con i propri tempi e inizialmente non sono sincronizzati. Ogni orologio può essere implementato con un semplice contatore software, incrementato di un valore specifico ogni unità di tempo. Tuttavia, il valore con cui un orologio viene incrementato differisce per processo: 1 per A, 5 per B e 2 per C.

Al tempo 1, A invia il messaggio m1 a B. Al momento dell’arrivo, l’orologio a B legge 10 nel suo orologio interno. Poiché il messaggio è stato inviato è stato timestampato con il tempo 1, il valore 10 nel processo B è certamente possibile (possiamo dedurre che ci sono voluti 9 tick per arrivare a B da A).

Considera ora il messaggio m2. Lascia B alle 15 e arriva a C alle 8. Questo valore di clock a C è chiaramente impossibile poiché il tempo non può andare indietro. Da * * e il fatto che m2 parte a 15, deve arrivare a 16 o più tardi. Pertanto, dobbiamo aggiornare il valore del tempo corrente in C per essere più grande di 15 (aggiungiamo +1 al tempo per semplicità). In altre parole, quando arriva un messaggio e l’orologio del ricevitore mostra un valore che precede il timestamp che individua la partenza del messaggio, il ricevitore inoltra velocemente il suo orologio per essere un’unità di tempo in più rispetto all’ora di partenza. Nella figura 6, vediamo che m2 ora corregge il valore dell’orologio da C a 16. Allo stesso modo, m3 e m4 arrivano rispettivamente a 30 e 36.

Dall’esempio precedente, Maarten van Steen et al formula l’algoritmo di Lamport come segue:

1. Prima di eseguire un evento (ad esempio l’invio di un messaggio sulla rete, …), p incre incrementa c C: c

2. Quando il processo p sends invia il messaggio m al processo Pj, imposta il timestamp ts(m) di m uguale a c after dopo aver eseguito il passaggio precedente.

3. Al ricevimento di un messaggio m, il processo Pj regola il proprio contatore locale come Cj < – max{Cj, ts (m)} dopo di che esegue il primo passaggio e consegna il messaggio all’applicazione.

Orologi vettoriali

Ricorda alla definizione di Lamport della relazione “accade-prima”, se ci sono due eventi a e b tali che a si verifica prima di b, allora anche a è posizionato in quell’ordine prima di b, cioè C(a) < C(b). Tuttavia, ciò non implica una causalità inversa, poiché non possiamo dedurre che a preceda b semplicemente confrontando i valori di C(a) e C(b) (la prova è lasciata come esercizio al lettore).

Per ricavare maggiori informazioni sull’ordinamento degli eventi in base al loro timestamp, viene proposto Vector Clocks, una versione più avanzata dell’Orologio logico di Lamport. Per ogni processo pᵢ del sistema, l’algoritmo mantiene un vettore vcᵢ con i seguenti attributi:

1. vcᵢ: orologio logico locale a pᵢ, o il numero di eventi che si sono verificati prima del timestamp corrente.

2. Se vc = = k, p knows sa che gli eventi k si sono verificati a Pj.

L’algoritmo degli orologi vettoriali va quindi come segue:

1. Prima di eseguire un evento, p records registra un nuovo evento che si verifica da solo eseguendo vc

2. Quando p sends invia un messaggio m a Pj, imposta il timestamp ts (m) uguale a vcᵢ dopo aver eseguito il passaggio precedente.

3. Quando il messaggio m viene ricevuto, processo Pj aggiornare ogni k del proprio orologio vettoriale: VCj ← max { VCj, ts (m)}. Quindi continua a eseguire il primo passaggio e consegna il messaggio all’applicazione.

Da questi passaggi, quando un processo Pj riceve un messaggio m dal processo Pᵢ con timestamp ts(m), si conosce il numero di eventi che si sono verificati a Pᵢ casualmente preceduto l’invio di m. Inoltre, Pj conosce anche gli eventi che sono stati conosciuti per Pᵢ gli altri processi prima di inviare m. (Sì, questo è vero, se sei in materia di questo algoritmo per il Gossip Protocollo 🙂).

Speriamo che la spiegazione non ti lasci grattarti la testa troppo a lungo. Tuffiamoci in un esempio per padroneggiare il concetto:

In questo esempio, abbiamo tre processi p₁, P₂ e p alternatively che scambiano alternativamente messaggi per sincronizzare insieme i loro orologi. p sends invia il messaggio m1 al tempo logico vc V = (1, 0, 0) (passaggio 1) a P₂. P₂, dopo aver ricevuto m1 con timestamp ts (m1) = (1, 0, 0), regola il suo tempo logico VC₂ a (1, 1, 0) (passaggio 3) e invia il messaggio m2 a p with con timestamp (1, 2, 0) (passaggio 1). Allo stesso modo, il processo p₁ accetta il messaggio m2 da P₂, altera il suo orologio logico a (2, 2, 0) (passaggio 3), dopo di che invia il messaggio m3 a p at a (3, 2, 0). p adjusts regola il suo orologio su (3, 2, 1) (passaggio 1) dopo aver ricevuto il messaggio m3 da p₁. Successivamente, riceve il messaggio m4, inviato da P₂ a (1, 4, 0), e quindi regola il suo orologio a (3, 4, 2) (passaggio 3).

In base a come avanziamo velocemente gli orologi interni per la sincronizzazione, l’evento a precede l’evento b se per tutti k, ts(a) ≤ ts(b), e c’è almeno un indice k’ per cui ts(a) < ts(b). Non è difficile vedere che (2, 2, 0) precede (3, 2, 1), ma (1, 4, 0) e (3, 2, 0) possono entrare in conflitto tra loro. Pertanto, con gli orologi vettoriali, possiamo rilevare se esiste o meno una dipendenza causale tra due eventi qualsiasi.

Take away

Quando si tratta del concetto di tempo nel sistema distribuito, l’obiettivo primario è quello di raggiungere il corretto ordine degli eventi. Gli eventi possono essere posizionati in ordine cronologico con gli orologi fisici o in ordine logico con gli orologi logici di Lamtport e gli orologi vettoriali lungo la timeline di esecuzione.

Quali sono le prospettive?

Il prossimo capitolo della serie, esamineremo come la sincronizzazione dell’ora può fornire risposte sorprendentemente semplici ad alcuni problemi classici nei sistemi distribuiti: messaggi al massimo uno , coerenza della cache e reciproca esclusione .

Leslie Lamport: tempo, orologi e ordinamento degli eventi in un sistema distribuito. 1978.

Barbara Liskov: Usi pratici degli orologi sincronizzati nei sistemi distribuiti. 1993.

Maarten van Steen, Andrew S. Tanenbaum: Sistemi distribuiti. 2017.

Barbara Liskov, Liuba Shrira, John Wroclawski: Efficiente At-Most-Once messaggi basati su orologi sincronizzati. 1991.

Cary G. Gray, David R. Cheriton: Leases: un efficiente meccanismo Fault-Tolerant per la coerenza della cache dei file distribuiti. 1989.

Ricardo Gusella, Stefano Zatti: La precisione della sincronizzazione dell’orologio raggiunta da TEMPO in Berkeley UNIX 4.3 BSD. 1989.