Kompletter metrischer Raum

In der Mathematik ist ein vollständiger metrischer Raum ein metrischer Raum, in dem jede Cauchy-Sequenz konvergent ist. Mit anderen Worten, jede Cauchy-Sequenz im metrischen Raum tendiert in der Grenze zu einem Punkt, der wiederum ein Element dieses Raumes ist. Daher ist der metrische Raum in gewissem Sinne “vollständig.”

• 1 Formale Definition
• 2 Beispiele
• 3 Vervollständigung
  • 3.1 Beispiele
• 4 Topologisch kompletter Raum
• 5 Siehe auch

Formale Definition

Sei X ein metrischer Raum mit der Metrik d. Dann ist X vollständig, wenn für jede Cauchy-Sequenz 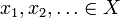ein Element 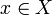vorhanden ist, so dass .

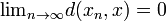Beispiele

• Die reellen Zahlen R und allgemeiner endlichdimensionale euklidische Räume mit der üblichen Metrik sind vollständig.
• Jeder kompakte metrische Raum ist sequentiell kompakt und daher vollständig. Das Gegenteil gilt nicht: Zum Beispiel ist R vollständig, aber nicht kompakt.
• In einem Raum mit der diskreten Metrik sind die einzigen Cauchy-Sequenzen diejenigen, die von einem bestimmten Punkt an konstant sind. Daher ist jeder diskrete metrische Raum vollständig. Daher sind einige begrenzte vollständige metrische Räume nicht kompakt.
• Die rationalen Zahlen Q sind nicht vollständig. Zum Beispiel ist die Sequenz (xn) definiert durch x0 = 1, xn+1 = 1 + 1 / xn ist Cauchy, konvergiert aber nicht in Q. (In R konvergiert es zu einer irrationalen Zahl.)

Vervollständigung

Jeder metrische Raum X hat eine Vervollständigung 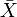, die ein vollständiger metrischer Raum ist, in den X isometrisch als dichter Unterraum eingebettet ist. Die Vollendung hat eine universelle Eigenschaft.

Beispiele

• Die reellen Zahlen R sind die Vervollständigung der rationalen Zahlen Q in Bezug auf die übliche Metrik der absoluten Entfernung.

Topologisch vollständiger Raum

Vollständigkeit ist keine topologische Eigenschaft: Es ist möglich, dass ein vollständiger metrischer Raum homöomorph zu einem metrischen Raum ist, der nicht vollständig ist. Zum Beispiel ist die reelle Linie R homöomorph zu einem offenen Intervall, sagen wir (0,1). Ein weiteres Beispiel: Die Karte

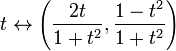
ist ein Homöomorphismus zwischen dem vollständigen metrischen Raum R und dem unvollständigen Raum, der der Einheitskreis in der euklidischen Ebene ist, wobei der Punkt (0,-1) gelöscht ist. Der letztere Raum ist nicht vollständig, da die Nicht-Cauchy-Sequenz, die t = n entspricht, wenn n durch die positiven ganzen Zahlen läuft, einer nicht konvergenten Cauchy-Sequenz auf dem Kreis zugeordnet ist.

Wir können einen topologischen Raum als metrisch topologisch vollständig definieren, wenn er homöomorph zu einem vollständigen metrischen Raum ist. Eine topologische Bedingung für diese Eigenschaft ist, dass der Raum metrisierbar ist und ein absolutes Gδ, dh ein Gδ in jedem topologischen Raum, in den er eingebettet werden kann (oder nur Gδ in seiner Vervollständigung in einer ausgewählten Metrik). Insbesondere sind alle offenen Teilmengen euklidischer Räume metrisch topologisch vollständig.

Siehe auch

• Banach-Raum
• Hilbert-Raum

Einige Inhalte auf dieser Seite sind möglicherweise zuvor auf Citizendium erschienen.