dodawanie wektorów
kiedy wspomnieliśmy we wstępie, że wektor jest albo uporządkowaną parą, albo trypletem liczb, domyślnie zdefiniowaliśmy wektory w kategoriach składników.
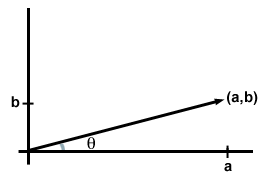
każdy wpis w 2-wymiarowej uporządkowanej parze (a, b) lub trójwymiarowej trójwymiarowej (a, b, c) nazywa się składową wektora. O ile nie określono inaczej, przyjmuje się zwykle, że pozycje odpowiadają liczbie jednostek, które wektor ma w kierunkach x, y i (w przypadku 3D) z płaszczyzny lub przestrzeni. Innymi słowy, możesz myśleć o składowych jako o współrzędnych punktu związanego z wektorem. (W pewnym sensie wektor jest punktem, chociaż kiedy rysujemy wektory, Zwykle rysujemy strzałkę od początku do punktu.)
dodawanie wektorów za pomocą elementów
biorąc pod uwagę dwa wektory u = (u1, u2) i v = (v1, v2) na płaszczyźnie euklidesowej, suma jest dana przez:
| u + v = (u1 + v1, u2 + v2) |
dla wektorów trójwymiarowych u = (u1, u2, u3) i v = (v1, v2, v3) wzór jest prawie identyczny:
| u + v = (u1+ v1, u2 + v2, u3 + v3) |
innymi słowy, dodawanie wektorów jest jak zwykłe dodawanie: składnik po składniku.
zauważ, że jeśli zsumujesz dwa wektory 2-wymiarowe, musisz otrzymać kolejny wektor 2-wymiarowy jako odpowiedź. Dodanie 3-wymiarowych wektorów da 3-wymiarowe odpowiedzi. Wektory 2-i 3-wymiarowe należą do różnych przestrzeni wektorowych i nie można ich dodawać. Te same zasady mają zastosowanie, gdy mamy do czynienia z mnożeniem skalarnym.