pełna przestrzeń metryczna

w matematyce przestrzeń metryczna zupełna jest przestrzenią metryczną, w której każdy ciąg Cauchy ‘ ego jest zbieżny. Innymi słowy, każdy ciąg Cauchy ‘ ego w przestrzeni metrycznej zmierza w granicy do punktu, który jest ponownie elementem tej przestrzeni. Stąd przestrzeń metryczna jest w pewnym sensie “zupełna.”

• 1 Definicja Formalna
• 2 Przykłady
• 3 zakończenie
  • 3.1 przykłady
• 4 przestrzeń topologiczna całkowita
• 5 Zobacz też

definicja Formalna

niech X będzie przestrzenią metryczną z metryką d. wtedy X jest zupełne, jeśli dla każdego ciągu Cauchy ‘ ego 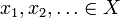istnieje element 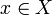taki, że .

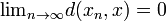przykłady

• liczby rzeczywiste R, a bardziej ogólnie skończone przestrzenie Euklidesowe, ze zwykłą metryką są kompletne.
• każda zwarta przestrzeń metryczna jest kolejno zwarta, a więc zupełna. Konwersja nie trzyma: na przykład R jest kompletny, ale nie zwarty.
• w przestrzeni z metryką dyskretną jedynymi ciągami Cauchy ‘ ego są te, które od pewnego momentu są stałe. Stąd każda Dyskretna przestrzeń metryczna jest zupełna. Tak więc niektóre ograniczone kompletne przestrzenie metryczne nie są zwarte.
• Liczby wymierne Q nie są kompletne. Na przykład ciąg (xn) zdefiniowany przez x0 = 1, xn+1 = 1 + 1/xn jest Cauchy, ale nie jest zbieżny w Q. (W R zbiega się do liczby irracjonalnej.)

dopełnienie

każda przestrzeń metryczna X ma dopełnienie 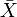, które jest zupełną przestrzenią metryczną, w której X jest izometrycznie osadzona jako gęsta podprzestrzeń. Zakończenie ma właściwość uniwersalną.

przykłady

• liczby rzeczywiste R są dopełnieniem liczb wymiernych Q względem zwykłej metryki odległości bezwzględnej.

przestrzeń topologiczna zupełna

kompletność nie jest własnością topologiczną: możliwe jest, że zupełna przestrzeń metryczna jest homeomorficzna z przestrzenią metryczną, która nie jest zupełna. Na przykład linia rzeczywista R jest homeomorficzna do przedziału otwartego, powiedzmy (0,1). Inny przykład: mapa

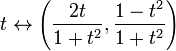
jest homeomorfizmem między zupełną przestrzenią metryczną R a przestrzenią niekompletną,która jest okręgiem jednostkowym na płaszczyźnie euklidesowej z usuniętym punktem (0, -1). Ta ostatnia przestrzeń nie jest kompletna, ponieważ ciąg nie-Cauchy ‘ego odpowiadający t=n, gdy n biegnie przez dodatnie liczby całkowite, jest odwzorowany na ciąg nie-Cauchy’ ego na okręgu.

możemy zdefiniować przestrzeń topologiczną jako metrycznie topologicznie zupełną, jeśli jest homeomorficzna do pełnej przestrzeni metrycznej. Warunkiem topologicznym dla tej własności jest to, że przestrzeń jest metryzowalna i bezwzględna Gδ, czyli Gδ w każdej przestrzeni topologicznej, w której może być osadzona (lub po prostu Gδ w jej dopełnieniu w wybranej metryce). W szczególności wszystkie otwarte podzbiory przestrzeni euklidesowych są metrycznie topologicznie kompletne.

Zobacz też

• przestrzeń Banacha
• przestrzeń Hilberta

niektóre treści na tej stronie mogły wcześniej pojawiać się na Citizendium.