punkty zdrowia trybików

by Posted on

trybiki mają określoną liczbę punktów zdrowia (HP) w zależności od ich poziomu. Tryby poziomu 1 mają najniższą ilość PW, podczas gdy tryby poziomu 12 mają najwyższą ilość PW.

poniższa tabela pokazuje, ile PW ma każdy poziom Cog i jakie Gagi mogą pokonać Cog w jednym trafieniu. Niektóre Gagi muszą być organiczne.

poziom punkty zdrowia jedno trafienie gagów
1 6 babeczka (6 obrażeń)
Doniczka (10 obrażeń)
Szklanka Wody (6 obrażeń)
2 12 skórka od Banana (12 obrażeń)
Squirt Gun (12 obrażeń)
Sandbag (18 obrażeń)
3 20 Grabie (20 obrażeń)
bagażnik słonia (21 obrażeń)
butelka Seltzer (21 obrażeń)
4 30 Wąż strażacki (30 obrażeń)
kowadło (30 obrażeń)
Kulki (35 uszkodzenia)
5 42 duża waga (45 obrażeń)
Organiczne ciasto z kremem (44 obrażeń)
Ruchome piaski (50 obrażeń)
6 56 sejf (60 uszkodzeń)
Zapadnia (70 uszkodzeń)
7 72 Organiczna Zapadnia (77 obrażeń)
Burza (80 obrażeń)
8 90 śpiewak operowy (90 obrażeń)
tort urodzinowy (100 obrażeń)
9 110 Ekologiczny tort urodzinowy (110)
Ekologiczny Gejzer (115 uszkodzenia)
10 132 Ekologiczny tort weselny (132))
11 156 fortepian (170 uszkodzeń)
TNT (180 uszkodzeń)
12 200 Kolej ekologiczna (214 uszkodzeń)

wzory

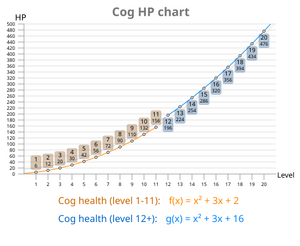
wykres pokazujący wzrost zdrowia trybików według ich poziomu. Różnica w zdrowiu trybików poziomu 12 jest widoczna.

wzór na zdrowie koła zębatego może być:

{\displaystyle f (x)=X^{2}+3x+2}

lub w uproszczeniu:

{\displaystyle f(x) = (x+1) \ times (X+2)}

gdzie x jest poziomem koła zębatego, a f (x) jest funkcją, która zwraca wartość zdrowia koła zębatego.

na przykład wzór działa w następującej metodzie dla trybików poziomu czwartego, które mają 30 HP:

{\displaystyle f(4)=(4+1)\czasy (4+2)} {\displaystyle f (4) = (5) \ times (6)} {\displaystyle f(4)=30}

powyższy wzór dotyczy każdego poziomu koła zębatego z wyjątkiem Poziomu 12, który ma 200 km.

aby pobrać poziom Cog z danego HP, zamiast pobierać HP z poziomu, można użyć wzoru kwadratowego, gdzie n to HP:

{\displaystyle x_{1,2} = {\frac {-3\pm {\sqrt {9-4*(2-n)}}}{2}}}

na przykład, równanie zostanie rozwiązane w następujący sposób, aby dowiedzieć się, który Cog miałby 156 HP:

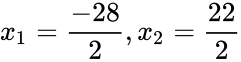
{\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9-4*(2-156)}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9-4*-154}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {9+616}}}{2}}} {\displaystyle x_{1,2}={\frac {-3\pm {\sqrt {625}}}{2}}} {\displaystyle x_{1,2}={\frac {-3 \ pm 25}{2}}} {\displaystyle x_{1}={\frac {-3-25}{2}},x_{2}={\frac {-3+25}{2}}} {\displaystyle x_{1} = {\frac {-28}{2}}, x_{2} = {\frac {22}{2}}} {\displaystyle x_{1}=-14, x_{2}=11}

ponieważ f (x) jest funkcją paraboli i Żadne z rozwiązań nie jest wartością minimalną funkcji, istnieją dwie odpowiedzi dla równania: -14, które nie jest rzeczywistym poziomem Cog; i 11, które jest rzeczywistym poziomem.

chociaż wzór ten działa dla wszystkich poziomów Cog, gdy wykracza poza regularne poziomy Cog, formuła ta zaczyna być nie do zastosowania w praktyce z powodu liczb zespolonych. Dla dowolnej wartości N mniejszej niż -0,25 równanie to wprowadza liczby zespolone, które nadal działają w teorii, ale nie w praktyce.

Ciekawostki

  • mimo że trybiki poziomu 12 powinny mieć 182 HP, zamiast tego mają 200, co jest zasadniczo 10% wzmocnieniem. Zgodnie ze wzorem, koło zębate o mocy 200 km powinno mieć poziom około 12,65 (lub około -15,65, choć wartości ujemne nie są zgodne z poziomem koła zębatego).
  • według wzoru Dyrektor ds. marketingu miałby 2652 HP, biorąc pod uwagę, że jest to Poziom 50.

Published by admin

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany.