Synchronizacja czasu w systemach rozproszonych

jeśli znasz takie strony jak facebook.com lub google.com, może nie mniej niż raz zastanawiałeś się, jak te strony internetowe mogą obsłużyć miliony, a nawet dziesiątki milionów żądań na sekundę. Czy istnieje jeden komercyjny serwer, który może wytrzymać tak ogromną liczbę żądań, w taki sposób, aby każde żądanie mogło być doręczone na czas użytkownikom końcowym?

nurkując głębiej w tę sprawę, docieramy do koncepcji systemów rozproszonych, zbioru niezależnych komputerów (lub węzłów), które wydają się swoim użytkownikom jako jeden spójny system. To pojęcie spójności dla użytkowników jest jasne, ponieważ uważają, że mają do czynienia z pojedynczą ogromną maszyną, która przybiera postać wielu procesów działających równolegle w celu obsługi partii żądań jednocześnie. Jednak dla ludzi, którzy rozumieją infrastrukturę systemową, sprawy nie okazują się takie proste.

w przypadku tysięcy niezależnych maszyn działających jednocześnie, które mogą obejmować wiele stref czasowych i kontynentów, niektóre rodzaje synchronizacji lub koordynacji muszą być podane, aby te maszyny efektywnie współpracowały ze sobą (aby mogły wyglądać jako jedna). W tym blogu omówimy synchronizację czasu i sposób, w jaki osiąga spójność między maszynami w zakresie porządkowania i przyczynowości zdarzeń.

treść tego bloga będzie zorganizowana następująco:

1. synchronizacja zegarów
2. Zegary logiczne
3. co dalej?

Zegary fizyczne

w systemie scentralizowanym czas jest jednoznaczny. Prawie wszystkie komputery mają “zegar czasu rzeczywistego”, aby śledzić czas, Zwykle zsynchronizowany z precyzyjnie obrobionym kryształem kwarcowym. W oparciu o dobrze zdefiniowaną oscylację częstotliwości tego kwarcu, system operacyjny komputera może precyzyjnie monitorować czas wewnętrzny. Nawet gdy komputer jest wyłączony lub gaśnie, kwarc nadal kleszczy ze względu na baterię CMOS, małą potęgę zintegrowaną z płytą główną. Gdy komputer łączy się z siecią (Internet), system operacyjny kontaktuje się z serwerem timera, który jest wyposażony w odbiornik UTC lub dokładny zegar, aby dokładnie zresetować lokalny timer za pomocą Network Time Protocol, zwanego również NTP.

chociaż ta częstotliwość kwarcu krystalicznego jest dość stabilna, nie można zagwarantować, że wszystkie kryształy różnych komputerów będą działać z dokładnie tą samą częstotliwością. Wyobraźmy sobie system z n komputerami, którego każdy kryształ działa z nieco inną szybkością, powodując stopniowe wyłączanie zegarów z synchronizacji i podawanie różnych wartości podczas odczytu. Spowodowana tym różnica w wartościach czasu nazywana jest pochyleniem zegara.

w tych okolicznościach zrobiło się nieprzyjemnie z powodu posiadania wielu rozdzielonych przestrzennie maszyn. Jeśli pożądane jest użycie wielu wewnętrznych zegarów fizycznych, jak zsynchronizować je z zegarami rzeczywistymi? Jak zsynchronizować je ze sobą?

Network Time Protocol

wspólne podejście do synchronizacji par między komputerami jest poprzez wykorzystanie modelu klient-serwer, tj. niech klienci kontaktują się z serwerem czasu. Rozważmy następujący przykład z 2 maszynami A i B:

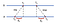
najpierw a wysyła żądanie o wartości T₀ do B. B, gdy wiadomość dotrze, rejestruje czas odbioru T₁ z własnego zegara lokalnego i odpowiedzi z czasem wiadomości oznaczonym T₂, zapisując wcześniej zarejestrowaną wartość T₁. Wreszcie, A, po otrzymaniu odpowiedzi od B, rejestruje czas przybycia T₃. Aby uwzględnić opóźnienie czasowe w dostarczaniu wiadomości, obliczamy Δ₁ = T₁-t₀, Δ₂ = T₃-t₂. Teraz szacunkowe przesunięcie A względem B wynosi:

w oparciu o θ, możemy albo spowolnić zegar A, albo zapiąć go tak, aby obie maszyny mogły być zsynchronizowane ze sobą.

ponieważ NTP ma zastosowanie w parze, Zegar B można dostosować do zegara A. Jednak nierozsądne jest ustawianie zegara w B, jeśli wiadomo, że jest bardziej dokładny. Aby rozwiązać ten problem, NTP dzieli serwery na warstwy, czyli serwery rankingowe, aby zegary z mniej dokładnych serwerów o mniejszych Rang były zsynchronizowane z dokładniejszymi serwerami o wyższych rang.

algorytm Berkeley

w przeciwieństwie do klientów, które okresowo kontaktują się z serwerem czasu w celu dokładnej synchronizacji czasu, Gusella i Zatti , w 1989 Berkeley Unix paper, zaproponował model klient-serwer, w którym serwer czasu (Demon) sonduje każdą maszynę okresowo zapytać, która godzina jest tam. W oparciu o odpowiedzi, oblicza czas podróży w obie strony wiadomości, uśredniając aktualny czas z nieznajomością wartości odstających w czasie i “mówi wszystkim innym maszynom, aby przyspieszyli swoje zegary do nowego czasu lub spowolnili swoje zegary, aż do osiągnięcia określonej redukcji haw”.

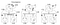
Zegary logiczne

cofnijmy się o krok i przemyślmy naszą bazę zsynchronizowanych znaczników czasu. W poprzedniej sekcji przypisujemy konkretne wartości do zegarów wszystkich uczestniczących maszyn, odtąd mogą one uzgodnić globalną oś czasu, w której zdarzenia mają miejsce podczas wykonywania systemu. Jednak to, co naprawdę ma znaczenie w całej osi czasu, to kolejność, w jakiej występują powiązane wydarzenia. Na przykład, jeśli w jakiś sposób musimy wiedzieć tylko to wydarzenie dzieje się wcześniej zdarzenia B, to nie ma znaczenia, jeśli Tₐ = 2, Tᵦ = 6 lub Tₐ = 4, Tᵦ = 10, aż Tₐ < Tᵦ. To przesuwa naszą uwagę na sferę zegarów logicznych, gdzie na synchronizację wpływa definicja Leslie Lamport relacji “dzieje się-przed”.

Zegary logiczne Lamporta

w swoim fenomenalnym dokumencie Time, Clocks, and the Order of Events in a Distributed System z 1978 roku Lamport zdefiniował relację “happens-before” → ” w następujący sposób:

1. Jeśli a i b są zdarzeniami w tym samym procesie, A a jest przed b, to a→b.

2. Jeśli a jest wysłaniem wiadomości przez jeden proces, A b jest odebraniem tej samej wiadomości przez inny proces, to a→b.

3. Jeśli A→B i b→c, to a → c.

Jeśli zdarzenia x, y występują w różnych procesach, które nie wymieniają komunikatów, ani X → Y, ani y → x nie są prawdziwe, x i y są uważane za współbieżne. Biorąc pod uwagę funkcję C, która przypisuje wartość czasu C(a) dla zdarzenia, na które zgadzają się wszystkie procesy, Jeśli a i b są zdarzeniami w tym samym procesie, A A występuje przed b, C(a) < C(b)*. Podobnie, jeśli A jest wysłaniem wiadomości przez jeden proces, A b jest odebraniem tej wiadomości przez inny proces, C (a) < C(b) **.

przyjrzyjmy się teraz algorytmowi zaproponowanemu przez Lamport do przypisywania czasów zdarzeniom. Rozważ następujący przykład z klastrem 3 procesów A, B, C:

Zegary tych 3 procesów działają na swoim własnym taktowaniu i są początkowo zsynchronizowane. Każdy zegar może być zaimplementowany za pomocą prostego licznika programowego, zwiększanego o określoną wartość co jednostki czasu T. Jednak wartość, o którą zwiększany jest zegar, różni się w zależności od procesu: 1 dla a, 5 dla B i 2 Dla C.

w czasie 1, A wysyła wiadomość m1 do B. w momencie przybycia zegar w B odczytuje 10 w swoim wewnętrznym zegarze. Ponieważ wiadomość została wysłana z czasem 1, wartość 10 w procesie B jest z pewnością możliwa (możemy wywnioskować, że otrzymanie B z A zajęło 9 tyknięć).

zastanów się teraz nad Komunikatem m2. Opuszcza B o 15 i dociera do C O 8. Ta wartość zegara w C jest wyraźnie niemożliwa, ponieważ czas nie może się cofnąć. Od * * i fakt, że m2 pozostawia w 15, musi dotrzeć do 16 lub później. Dlatego musimy zaktualizować aktualną wartość czasu w C, aby była większa niż 15 (dla uproszczenia dodajemy +1 do czasu). Innymi słowy, gdy wiadomość dotrze, a zegar odbiornika pokazuje wartość, która poprzedza znacznik czasu, który wskazuje odlot wiadomości, odbiornik szybko przekazuje swój zegar, aby był o jedną jednostkę czasu więcej niż czas odlotu. Na rysunku 6 widzimy, że m2 koryguje teraz wartość zegara w C do 16. Podobnie m3 i M4 osiągają odpowiednio 30 i 36.

na podstawie powyższego przykładu Maarten van Steen i wsp. formułują algorytm Lamporta w następujący sposób:

1. Przed wykonaniem zdarzenia (np. wysłaniem wiadomości przez sieć,…), pᵢ przyrosty Cᵢ: Cᵢ <- cᵢ + 1.

2. Gdy proces pᵢ wysyła wiadomość m do procesu PJ, ustawia znacznik czasu M ts (m) równy Cᵢ po wykonaniu poprzedniego kroku.

3. Po otrzymaniu wiadomości m, proces PJ dostosowuje swój własny licznik lokalny jako Cj < – max{CJ, ts (m)}, po czym wykonuje pierwszy krok i dostarcza wiadomość do aplikacji.

Zegary wektorowe

przypomnij sobie definicję relacji “dzieje się przed” Lamport, jeśli istnieją dwa zdarzenia a i b takie, że A występuje przed b, to a jest również umieszczone w tym porządku przed b, to jest C(a) < C(b). Nie oznacza to jednak odwrotnej przyczynowości, ponieważ nie możemy wywnioskować, że a idzie przed b jedynie przez porównanie wartości C(a) i C(b) (dowód pozostawiamy jako ćwiczenie czytelnikowi).

aby uzyskać więcej informacji na temat kolejności zdarzeń na podstawie ich znacznika czasu, proponuje się Zegary wektorowe, bardziej zaawansowaną wersję zegara logicznego Lamporta. Dla każdego procesu Pᵢ systemu algorytm utrzymuje wektor VCᵢ o następujących atrybutach:

1. VCᵢ: lokalny zegar logiczny w Pᵢ lub liczba zdarzeń, które miały miejsce przed bieżącym znacznikiem czasu.

2. Jeśli VCᵢ = k, Pᵢ wie, że zdarzenia k miały miejsce w Pj.

algorytm zegarów wektorowych wygląda wtedy następująco:

1. Przed wykonaniem zdarzenia, Pᵢ rejestruje nowe zdarzenie samo w sobie, wykonując vcᵢ <- VCᵢ + 1.

2. Gdy Pᵢ wysyła wiadomość m do Pj, ustawia znacznik czasu ts (m) równy VCᵢ po wykonaniu poprzedniego kroku.

3. Po odebraniu wiadomości m, proces PJ aktualizuje każdy k własnego zegara wektorowego: VCJ ← max { VCJ, ts(m)}. Następnie kontynuuje wykonywanie pierwszego kroku i dostarcza wiadomość do aplikacji.

wykonując te kroki, gdy proces PJ otrzymuje wiadomość m od procesu pᵢ ze znacznikiem czasu ts (m), zna liczbę zdarzeń, które miały miejsce w Pᵢ przypadkowo poprzedzone wysłaniem m. ponadto, PJ wie również o zdarzeniach, które były znane Pᵢ o innych procesach przed wysłaniem m. (Tak, to prawda, jeśli odnosisz ten algorytm do protokołu Plotkarskiego🙂).

mam nadzieję, że wyjaśnienie nie pozostawi cię zbyt długo na drapaniu się po głowie. Przyjrzyjmy się przykładowi, aby opanować tę koncepcję:

w tym przykładzie mamy trzy procesy P₁, P₂ i p₃ alternatywnie wymieniające wiadomości w celu zsynchronizowania ich zegarów. P₁ wysyła wiadomość m1 w czasie logicznym VC₁ = (1, 0, 0) (Krok 1) do P₂. P₂, po otrzymaniu m1 ze znacznikiem czasu ts (m1) = (1, 0, 0), dostosowuje swój logiczny czas VC₂ do (1, 1, 0) (Krok 3) i wysyła wiadomość m2 z powrotem do P₁ ze znacznikiem czasu (1, 2, 0) (Krok 1). Podobnie, proces p₁ przyjmuje wiadomość m2 z P₂, zmienia swój zegar logiczny na (2, 2, 0) (Krok 3), po czym wysyła wiadomość M3 do p₃ at (3, 2, 0). P₃ dostosowuje swój zegar do (3, 2, 1) (Krok 1) po otrzymaniu wiadomości m3 od P₁. Później przyjmuje wiadomość m4, wysyłaną przez P₂ at (1, 4, 0), a tym samym dostosowuje swój zegar do (3, 4, 2) (Krok 3).

opierając się na tym, jak przewijamy wewnętrzne zegary do synchronizacji, Zdarzenie a poprzedza Zdarzenie B, jeśli dla wszystkich k, ts(a) ≤ ts(B), i istnieje co najmniej jeden indeks k’, dla którego ts(a) < ts(B). Nietrudno zauważyć, że (2, 2, 0) poprzedza (3, 2, 1), ale (1, 4, 0) i (3, 2, 0) mogą ze sobą kolidować. Dlatego za pomocą zegarów wektorowych możemy wykryć, czy istnieje zależność przyczynowa między dowolnymi dwoma zdarzeniami.

Take away

jeśli chodzi o pojęcie czasu w systemie rozproszonym, podstawowym celem jest osiągnięcie właściwej kolejności zdarzeń. Zdarzenia mogą być umieszczane w porządku chronologicznym z zegarami fizycznymi lub w porządku logicznym z zegarami logicznymi Lamtport i zegarami wektorowymi wzdłuż osi czasu wykonania.

co dalej?

następnie w serii omówimy, w jaki sposób Synchronizacja czasu może zapewnić zaskakująco proste odpowiedzi na niektóre klasyczne problemy w systemach rozproszonych: co najwyżej jedno wiadomości, spójność pamięci podręcznej i wzajemne wykluczenie .

Leslie Lamport: czas, zegary i kolejność zdarzeń w systemie rozproszonym. 1978.

Barbara Liskov: praktyczne zastosowania zegarów synchronicznych w systemach rozproszonych. 1993.

Maarten van Steen, Andrew S. Tanenbaum: systemy rozproszone. 2017.

Barbara Liskow, Liuba Shrira, Jan Wrocławski: Wydajne co najwyżej raz wiadomości oparte na zsynchronizowanych zegarach. 1991.

Cary G. Gray, David R. Cheriton: Leases: an Efficient Fault-Tolerant Mechanism for Distributed File Cache consistence. 1989.

Ricardo Gusella, Stefano Zatti: dokładność synchronizacji zegara osiągnięta przez TEMPO w Berkeley UNIX 4.3 BSD. 1989.