Completo métrica de espaço

Em matemática, um completo espaço métrico é um espaço métrico em que toda sequência de Cauchy é convergente. Em outras palavras, cada sequência de Cauchy no espaço métrico tende no limite a um ponto que é novamente um elemento desse espaço. Portanto, o espaço métrico é, em certo sentido, “completo.”

• 1 definição Formal
• 2 Exemplos
• 3 Conclusão
  • 3.1 Exemplos
• 4 Topologicamente completo espaço
• 5 Veja também

Definição Formal

Deixe X ser um espaço métrico com a métrica d. Então X é completo se, para cada sequência de Cauchy 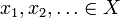existe um elemento 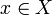tais que .

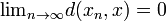Examples

• The real numbers R, and more generally finite-dimensional Euclidean spaces, with the usual metric are complete.
• qualquer espaço métrico compacto é sequencialmente compacto e, portanto, completo. O inverso não é válido: por exemplo, R é completo, mas não compacto.
• num espaço com a métrica discreta, as únicas sequências de Cauchy são aquelas que são constantes de algum ponto em diante. Portanto, qualquer espaço métrico discreto está completo. Assim, alguns espaços métricos completos delimitados não são compactos.
• os números racionais Q não estão completos. Por exemplo, a sequência (xn) definida por x0 = 1, xn+1 = 1 + 1/xn é Cauchy, mas não converge em Q. (em R converge para um número irracional.)

completação

todo espaço métrico X tem uma completação 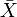que é um espaço métrico completo no qual X é isometricamente embutido como um subespaço denso. A conclusão tem uma propriedade universal.

Examples

• The real numbers R are the completion of the rational numbers Q with respect to the usual metric of absolute distance.

espaço topologicamente completo

Completude não é uma propriedade topológica: é possível que um espaço métrico completo seja homeomórfico a um espaço métrico que não está completo. Por exemplo, a linha real R é homeomórfica a um intervalo aberto, digamos, 0,1. Outro exemplo: o mapa

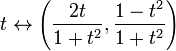
é um homeomorfismo entre o espaço métrico completo R e o espaço incompleto que é o círculo unitário no plano euclidiano com o ponto (0,-1) eliminado. Este último espaço não é completo, pois a sequência não-Cauchy correspondente a t=n Como n corre através dos inteiros positivos é mapeada para uma seqüência de Cauchy não-convergente no círculo.

podemos definir um espaço topológico para ser métricamente topologicamente completo se for homeomórfico a um espaço métrico completo. Um topológica condição para esta propriedade é de que o espaço ser metrizable e absoluta Gδ, isto é, um Gδ em cada espaço topológico no qual ele pode ser incorporado (ou apenas Gδ em sua conclusão em uma métrica escolhida). Em particular, todos os subconjuntos abertos de espaços euclidianos são metricamente topologicamente completos.

Veja também:

• espaço de Banach
• espaço de Hilbert

parte do conteúdo desta página pode anteriormente ter aparecido no Citizendium.